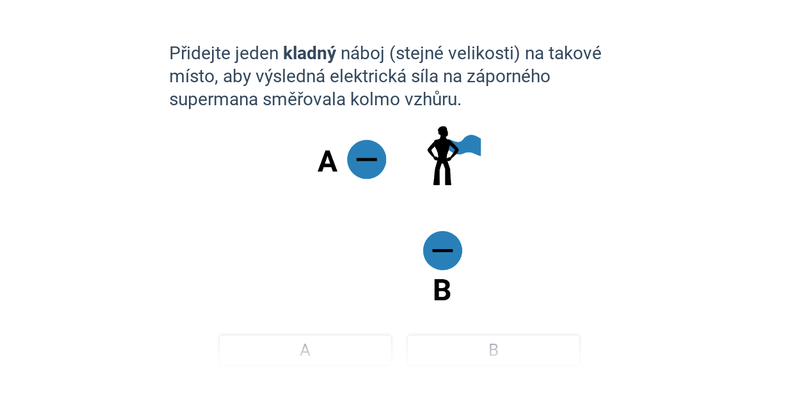
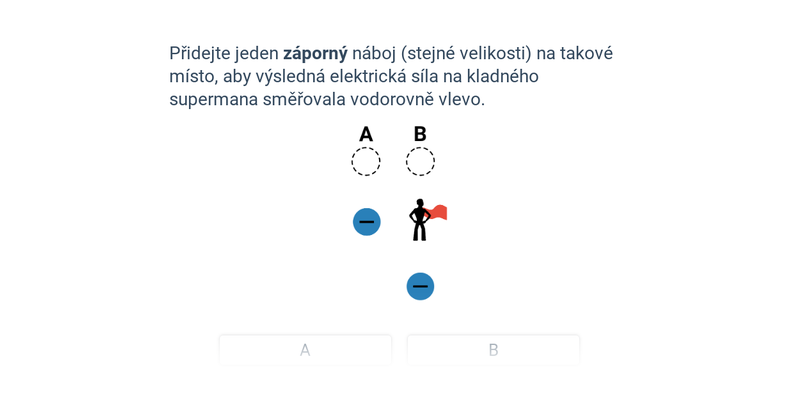
Mezi dvěma náboji (q_1 a q_2) působí elektrostatická síla F_\mathrm e=\frac{1}{4\pi \varepsilon}\frac{q_1\cdot q_2}{r^2} (ve vakuu F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2}). Protože je r ve jmenovateli (a ve druhé mocnině), bude se vzdáleností síla F_\mathrm e klesat. Například na dvojnásobnou vzdálenost bude síla čtvrtinová.
Pokud je nábojů více, zjistíme jednotlivé síly na náboj q_1 (nebo intenzity elektrického pole E v místě, kam bychom nějaký náboj mohli umístit) od ostatních nábojů a ty pak skládáme.
Příklad: druhý náboj nulovač intuitivně
Jaký náboj na místě otazníku způsobí nulovou výslednou sílu na list papíru?
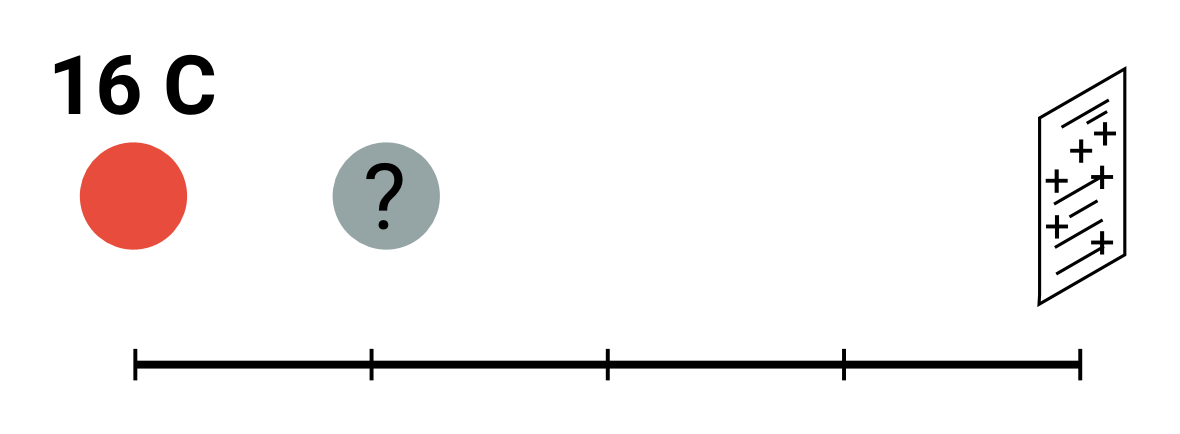
- Musí jít o záporný náboj (aby přitažlivost vyrovnávala odpuzování kladného listu a kladného náboje)
- Vzdálenosti od papíru jsou 4:3. Podle vzorce F_\mathrm e jsou účinky stejného náboje z těchto vzdáleností v poměru \frac{1}{4^2}:\frac{1}{3^2}.
- Aby byly obě působení stejná musíme tento poměr vyrovnat, různou velikostí nábojů.
- Náboje tedy budou v poměru 16:9.
Hledaný náboj je −9 C.
Příklad: druhý náboj nulovač pedantsky
Jaký náboj na místě otazníku způsobí nulovou výslednou sílu na list papíru?
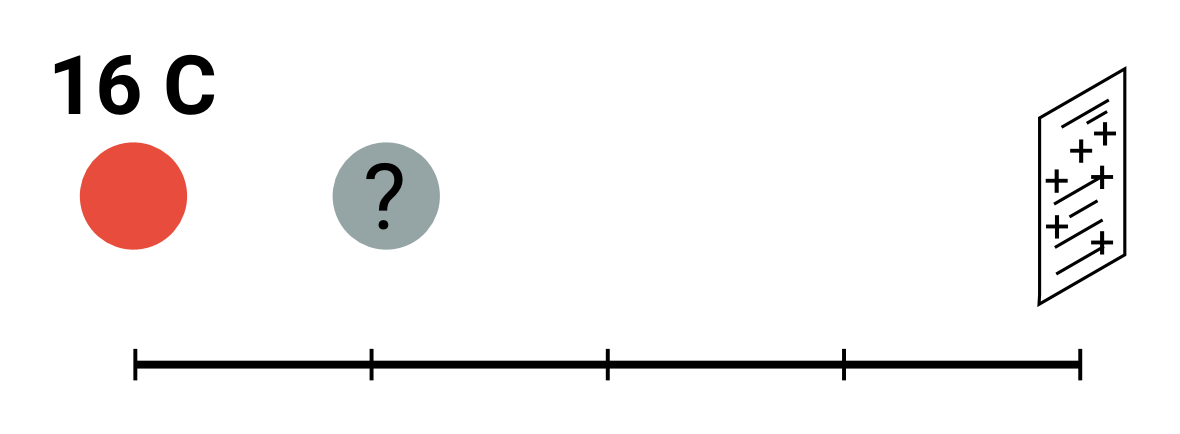
- Kladný náboj q_{+}=16\,\mathrm C odpuzuje ze vzdálenosti 4r_0 kladný papír q_\mathrm p silou F_\mathrm {e,+}.
- Aby výsledná síla vůbec mohla být nula, hledáme přitažlivou sílu. Bude tam tedy záporný náboj q_{-} ve vzdálenosti 3r_0.
- Aby výsledná síla opravdu byla nula, musí být velikost této síly F_\mathrm {e,-} stejně velká.
- F_\mathrm {e,+}=-F_\mathrm {e,-}
- Podle vzorce F_\mathrm e to je \frac{1}{4\pi \varepsilon_0}\frac{q_+\cdot q_\mathrm p}{(4r_0)^2}=-\frac{1}{4\pi \varepsilon_0}\frac{q_-\cdot q_\mathrm p}{(3r_0)^2}.
- Krátíme stejné členy: \color{red}{\frac{1}{4\pi \varepsilon_0}}\color{black}{\frac{q_+\cdot \color{red}{q_\mathrm p}}{4^2\cdot\color{red}{ r_0^2}}}=-\color{red}{\frac{1}{4\pi \varepsilon_0}}\color{black}{\frac{q_-\cdot \color{red}{q_\mathrm p}}{(3^2\cdot\color{red}{r_0^2})}}
- Zbývá tedy \frac{q_+}{16}=-\frac{q_-}{9}
- Vyjádříme hledaný q_-=-\frac{9}{16}\cdot q_{+}
q_{-}=-\frac{9}{16}\cdot 16\,\mathrm C, tedy −9 C.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.