Coulombova síla ve vakuu – 3. střední škola

Empiricky zjištěným Coulombovým zákonem popisujeme elektrickou (Coulombovu) síla F_\mathrm e, působící mezi dvěma bodovými (nebo kulově symetrickými) elektrickými náboji. Velmi se podobá Newtonovu gravitačnímu zákonu (F_\mathrm g=G\frac{m_1\cdot m_2}{r^2}), je dalekodosahová a bezdotyková, jen zde místo hmotností vystupují velikosti nábojů q_1 a q_2.

F_\mathrm e=k\frac{q_1\cdot q_2}{r^2}

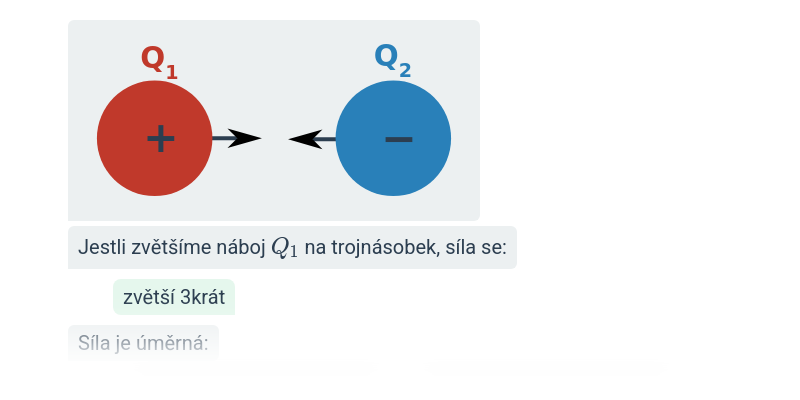
I zde síly směřují do středu druhého náboje a jsou stejně velké (akce a reakce). Mohou ale také směřovat od sebe – na rozdíl od gravitační síly totiž může být elektrická síla přitažlivá (různá znaménka náboje) i odpudivá (stejná znaménka náboje).

Tzv. Coulombova konstanta k, kterou zlomek násobíme má velikost 9 \cdot 10^9 \ \mathrm{N \cdot m^{2} \cdot C^{-2}} . Ve skutečnosti je rovna \frac{1}{4\pi \varepsilon_0}, kde \varepsilon_0 je jiná konstanta, tzv. permitivita vakua.

F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2}

Takže:

• Pokles jednoho náboje (např.q_1) na polovinu znamená pokles síly na polovinu
• Pokud budou oba náboje trojnásobné, budeme sílu násobit třemi za každý z nich. Bude tedy devítinásobná.
• Pokud stejné náboje vzdálíme na dvojnásobnou vzdálenost, bude síla čtvrtinová (děleno 2 na druhou).

Tyto vzorce platí kromě vakua skoro přesně i pro vzduch a většinu plynů (málo molekul ve velkém prostoru). V jiných materiálech musíme výpočet upravit o vliv materiálu, tzv. permitivitu prostředí a počítat i s ní.

Elektrické síly mezi nabitými objekty bývají jsou mnohem silnější než ty gravitační. Např. dvě koule o náboji 1 C by se na 1 m odpuzovaly silou 9 giganewtonů. Ještě štěstí, že je celkový náboj velkých objektů ve vesmíru (planet, hvězd, …) většinou prakticky nulový (stejné množství kladného a záporného náboje). Jinak bychom nějakou gravitaci skoro neřešili.