Výpis souhrnů
Elektrostatika
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Elektrostatika
Elektrostatika studuje elektrické působení, které je statické (v čase se nemění).
Toto působení způsobují elektrické náboje, které značíme písmenem q (a případně různými indexy) a mohou být kladné (+), nebo záporné (−). Přitom dva opačné náboje se přitahují a souhlasné odpuzují, podobně jako póly magnetů.
- Coulombova síla ve vakuu – Základní kvantitativní vztah pro silové působení mezi náboji. Velmi se podobá Newtonovu gravitačnímu zákonu.
- Coulombova síla v látkách a permitivita – Elektrické síly pro náboje obklopené číkoliv jiným než vakuem se liší o tzv. permitivitu.
- Elektrické pole a intenzita – Elektrické pole představuje mapu možného působení určitého náboje na ostatní náboje v okolí.
- Elektrické síly více nábojů – Další procvičení Coulombových sil a jejich skládání.
Coulombova síla ve vakuu
Empiricky zjištěným Coulombovým zákonem popisujeme elektrickou (Coulombovu) síla F_\mathrm e, působící mezi dvěma bodovými (nebo kulově symetrickými) elektrickými náboji. Velmi se podobá Newtonovu gravitačnímu zákonu (F_\mathrm g=G\frac{m_1\cdot m_2}{r^2}), je dalekodosahová a bezdotyková, jen zde místo hmotností vystupují velikosti nábojů q_1 a q_2.
F_\mathrm e=k\frac{q_1\cdot q_2}{r^2}
I zde síly směřují do středu druhého náboje a jsou stejně velké (akce a reakce). Mohou ale také směřovat od sebe – na rozdíl od gravitační síly totiž může být elektrická síla přitažlivá (různá znaménka náboje) i odpudivá (stejná znaménka náboje).
Tzv. Coulombova konstanta k, kterou zlomek násobíme má velikost 9 \cdot 10^9 \ \mathrm{N \cdot m^{2} \cdot C^{-2}} . Ve skutečnosti je rovna \frac{1}{4\pi \varepsilon_0}, kde \varepsilon_0 je jiná konstanta, tzv. permitivita vakua.
F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2}
Takže:
- Pokles jednoho náboje (např.q_1) na polovinu znamená pokles síly na polovinu
- Pokud budou oba náboje trojnásobné, budeme sílu násobit třemi za každý z nich. Bude tedy devítinásobná.
- Pokud stejné náboje vzdálíme na dvojnásobnou vzdálenost, bude síla čtvrtinová (děleno 2 na druhou).
Tyto vzorce platí kromě vakua skoro přesně i pro vzduch a většinu plynů (málo molekul ve velkém prostoru). V jiných materiálech musíme výpočet upravit o vliv materiálu, tzv. permitivitu prostředí a počítat i s ní.
Elektrické síly mezi nabitými objekty bývají jsou mnohem silnější než ty gravitační. Např. dvě koule o náboji 1 C by se na 1 m odpuzovaly silou 9 giganewtonů. Ještě štěstí, že je celkový náboj velkých objektů ve vesmíru (planet, hvězd, …) většinou prakticky nulový (stejné množství kladného a záporného náboje). Jinak bychom nějakou gravitaci skoro neřešili.
NahoruCoulombova síla v látkách a permitivita
Permitivita \varepsilon je vlastnost prostředí určující jak silné jsou v daném prostředí elektrické síly a elektrická pole. Obvykle ji definujeme jen pro nevodivé materiály (izolanty, čili dielektrika). Má jednotku \mathrm{F/m}, tedy farad na metr. V základních jednotkách SI je to dokonce \mathrm{C^{2} \cdot N^{-1} \cdot m^{-2}}.
Ve volném prostoru (vakuu) definujeme fyzikální konstantu – permitivitu vakua \varepsilon_0. Vystupuje v základním vzorci elektrické síly ve vakuu F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2} a má hodnotu 8{,}85 \cdot 10^{-12}\,\mathrm{F/m}.
Protože je hodnota permitivity vakua takové malé a složité číslo a u jiných materiálů to je podobné, zavedl se bezrozměrný násobitel – relativní permitivita \varepsilon_\mathrm r. O permitivitě ostatních materiálů pak většinou mluvíme v \varepsilon_\mathrm r-násobcích \varepsilon_\mathrm 0.
\varepsilon=\varepsilon_0 \cdot \varepsilon_\mathrm r
- Vzduch má permitivitu podobnou vakuu, jen 1,006x větší. (\varepsilon_\mathrm r=1{,}006)
- Voda má vysokou permitivitu, 81x větší než vakuum. (\varepsilon_\mathrm r=81)
- Ethanol má také vysokou relativní permitivitu. (\varepsilon_\mathrm r=24)
- Hodně materiálů a látek (např. oleje) má relativní permitivitu kolem 2 až 3.
Všechny běžné materiály mají relativní permitivitu větší než 1. Jen plazma se chová jako prostředí s relativní permitivitou nižší než ve vakuu.
Coulombovy síly v látkách jsou rovny:
F_\mathrm e=\frac{1}{4\pi \varepsilon}\frac{q_1\cdot q_2}{r^2}
Případně pokud místo \varepsilon dosadíme \varepsilon_0 \cdot \varepsilon_\mathrm r dostaneme:
F_\mathrm e=\frac{1}{4\pi \varepsilon_0 \cdot \varepsilon_\mathrm r}\frac{q_1\cdot q_2}{r^2}
V posledním vzorci se \varepsilon_\mathrm r nachází ve jmenovateli. Takže relativní permitivita vlastně udává, kolikrát jsou elektrické síly v materiálu slabší než ve vakuu:
- Voda má \varepsilon_\mathrm r=81, takže třeba elektrická síla, která by měla ve vakuu velikost 162 N, se ve vodě zmenší na 2 N.
Elektrické síly: více nábojů
Mezi dvěma náboji (q_1 a q_2) působí elektrostatická síla F_\mathrm e=\frac{1}{4\pi \varepsilon}\frac{q_1\cdot q_2}{r^2} (ve vakuu F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2}). Protože je r ve jmenovateli (a ve druhé mocnině), bude se vzdáleností síla F_\mathrm e klesat. Například na dvojnásobnou vzdálenost bude síla čtvrtinová.
Pokud je nábojů více, zjistíme jednotlivé síly na náboj q_1 (nebo intenzity elektrického pole E v místě, kam bychom nějaký náboj mohli umístit) od ostatních nábojů a ty pak skládáme.
Příklad: druhý náboj nulovač intuitivně
Jaký náboj na místě otazníku způsobí nulovou výslednou sílu na list papíru?
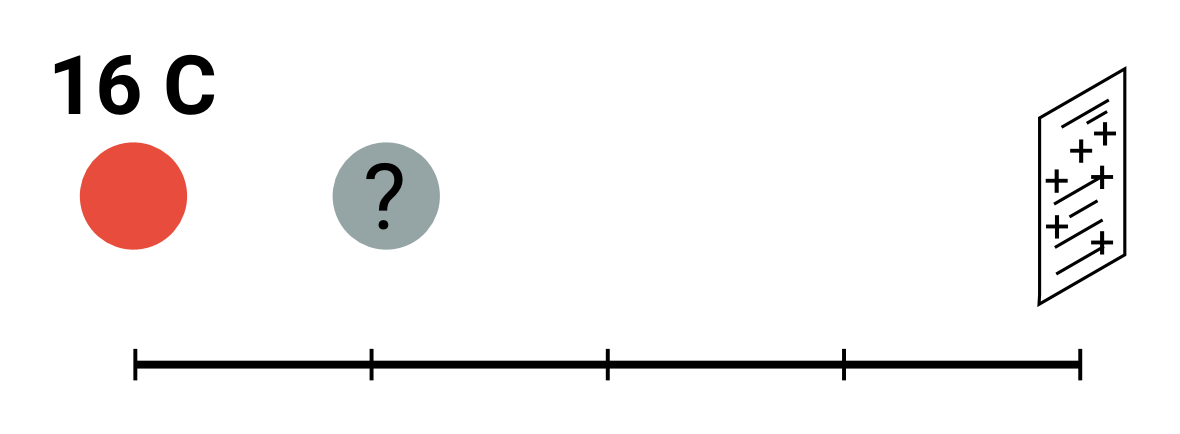
- Musí jít o záporný náboj (aby přitažlivost vyrovnávala odpuzování kladného listu a kladného náboje)
- Vzdálenosti od papíru jsou 4:3. Podle vzorce F_\mathrm e jsou účinky stejného náboje z těchto vzdáleností v poměru \frac{1}{4^2}:\frac{1}{3^2}.
- Aby byly obě působení stejná musíme tento poměr vyrovnat, různou velikostí nábojů.
- Náboje tedy budou v poměru 16:9.
Hledaný náboj je −9 C.
Příklad: druhý náboj nulovač pedantsky
Jaký náboj na místě otazníku způsobí nulovou výslednou sílu na list papíru?
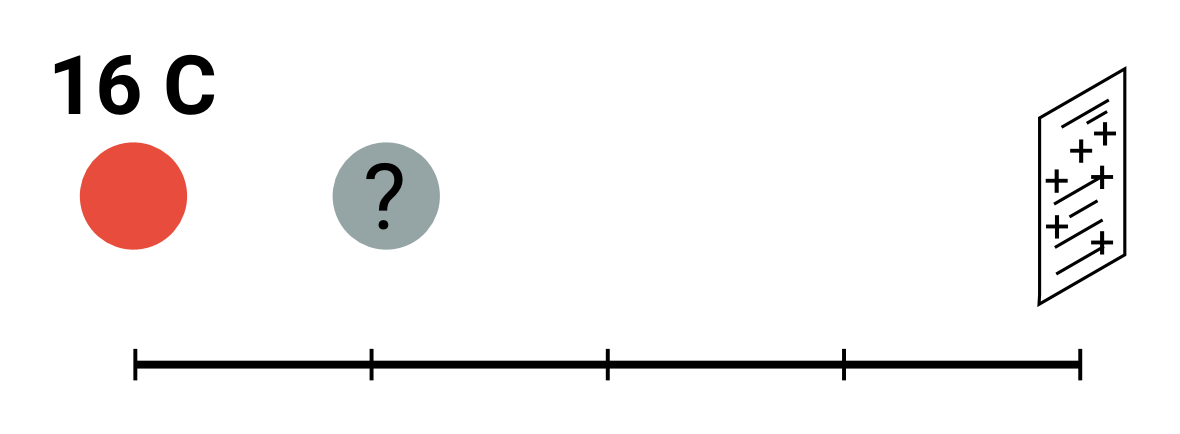
- Kladný náboj q_{+}=16\,\mathrm C odpuzuje ze vzdálenosti 4r_0 kladný papír q_\mathrm p silou F_\mathrm {e,+}.
- Aby výsledná síla vůbec mohla být nula, hledáme přitažlivou sílu. Bude tam tedy záporný náboj q_{-} ve vzdálenosti 3r_0.
- Aby výsledná síla opravdu byla nula, musí být velikost této síly F_\mathrm {e,-} stejně velká.
- F_\mathrm {e,+}=-F_\mathrm {e,-}
- Podle vzorce F_\mathrm e to je \frac{1}{4\pi \varepsilon_0}\frac{q_+\cdot q_\mathrm p}{(4r_0)^2}=-\frac{1}{4\pi \varepsilon_0}\frac{q_-\cdot q_\mathrm p}{(3r_0)^2}.
- Krátíme stejné členy: \color{red}{\frac{1}{4\pi \varepsilon_0}}\color{black}{\frac{q_+\cdot \color{red}{q_\mathrm p}}{4^2\cdot\color{red}{ r_0^2}}}=-\color{red}{\frac{1}{4\pi \varepsilon_0}}\color{black}{\frac{q_-\cdot \color{red}{q_\mathrm p}}{(3^2\cdot\color{red}{r_0^2})}}
- Zbývá tedy \frac{q_+}{16}=-\frac{q_-}{9}
- Vyjádříme hledaný q_-=-\frac{9}{16}\cdot q_{+}
q_{-}=-\frac{9}{16}\cdot 16\,\mathrm C, tedy −9 C.

