Mechanickou energii dělíme na dvě části. Potenciální (polohovou) E_\mathrm p a kinetickou (pohybovou) E_\mathrm k.
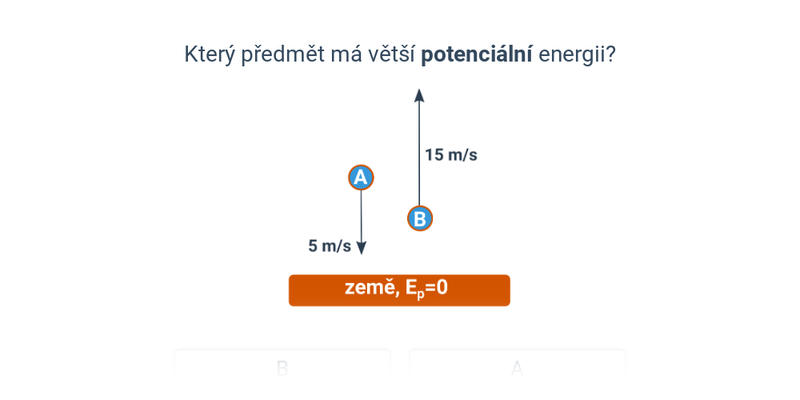
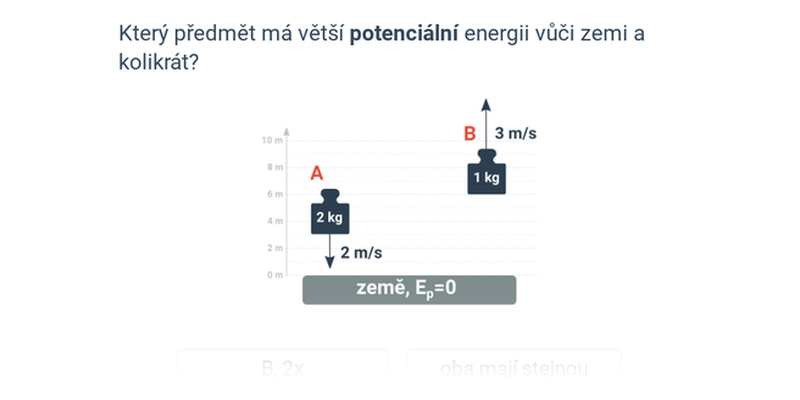
Potenciální energie
Je v homogenním tíhovém poli Země úměrná výšce nad zemí h podle vzorce:
E_\mathrm p=mgh
Není jednoznačná. Záleží na definici nulové výšky (obvykle úroveň podlahy/země). Např. 0,5kg polštář může ze stejného okraje balkonu spadnout:
dovnitř balkonu (pak h\approx 1\,\mathrm m a E_\mathrm p\approx 5\,\mathrm J)
ven přes okraj a padat 4 patra dolů (pak dává smysl definovat nulovou výšku až na chodníku a tím pádem je h\approx 13\,\mathrm m s E_\mathrm p\approx 65\,\mathrm J).
Kinetická energie
Pro hmotný bod (nebo nerotující těleso) je úměrná druhé mocnině rychlosti:
E_\mathrm k=\frac{1}{2}mv^2
V klidu je tedy nulová. Protože se zvedá s druhou mocninou rychlosti, znamená to, že vůči rychlosti nejde o přímou úměru:
- rychlost v se zvýší na 2násobek → E_\mathrm k se zvýší na 2²násobek, tedy 4krát
- rychlost v se zvýší na 5násobek→ E_\mathrm k se zvýší na 5²násobek, tedy 25krát
- rychlost v klesne na 1/2 → E_\mathrm k klesne na 1/2²násobek, tedy na 1/4
Vůči hmotnosti ale o přímou úměru jde:
- hmotnost m se zvýší na 3násobek → E_\mathrm k vzroste na 3násobek
- hmotnost m klesne na 1/10 → E_\mathrm k klesne na 1/10
Takže jak se změní E_\mathrm k, když hmotnost klesne na třetinu, ale rychlost vzroste dvakrát? Musíme ji vynásobit součinem 1/3 krát 2². Tedy vzroste na \frac{4}{3}E_\mathrm k.
Kinetická energie balvanu
Balvan o m=10\,\mathrm{kg} se uvolnil a valí se z kopce.
- Na začátku má v=0\,\mathrm{m/s} proto je E_\mathrm k=0\,\mathrm J.
- Po chvíli se rozjede na v=2\,\mathrm{m/s} a má E_\mathrm k=\frac{1}{2}\cdot 10\cdot 2^2\,\mathrm J=20\,\mathrm J.
- Do údolí dorazí rychlostí v=4\,\mathrm{m/s} a tedy s kinetickou energií E_\mathrm k=\frac{1}{2}\cdot 10\cdot 4^2\,\mathrm J=80\,\mathrm J.
Když těleso rotuje má tato kinetická energie ještě jednu složku \frac{1}{2}J\omega^2, tou se zde ale nezabýváme, často ji totiž můžeme zanedbat.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.