Výpis souhrnů
Práce, výkon, energie
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Práce, výkon, energie
Energii vnímáme jako míru schopnosti něco udělat. Stejně tak i ve fyzice – energie tělesa je definovaná jako jeho schopnost konat práci. Energie může mít různé formy a obecně se neztrácí, jen přeměňuje do jiných forem (její množství se zachovává).
- V mechanice se nejčastěji setkáme s energií pohybu nebo polohy, jinak řečeno kinetickou a potenciální.
- Součet kinetické a potenciální energie tělesa označujeme jako mechanickou energii tělesa.
- Když se přeměňují jen potenciální a kinetická energie tělesa nebo více těles mezi sebou, jde o zákon zachování mechanické energie.
Tělesa, která mají uloženou energii (např. pohybu), mohou vykonávat nějaké činnosti:
- Množství spotřebované (přeměněné) energie při vykonání úkolu odpovídá práci.
- Pokud konání práce trvalo nějakou dobu, můžeme určit jak rychle práce probíhala – rychlost výkonu práce je výkon.
- Ne vždy se všechna energie přemění na to co chceme (např. u žárovky se kromě svícení přemění spousta energie na teplo). Poměr mezi výkonem, který chceme a dodávaným výkonem (příkonem) je účinnost.
Kinetická a potenciální energie
Mechanickou energii dělíme na dvě části. Potenciální (polohovou) E_\mathrm p a kinetickou (pohybovou) E_\mathrm k.
Potenciální energie
Je v homogenním tíhovém poli Země úměrná výšce nad zemí h podle vzorce:
E_\mathrm p=mgh
Není jednoznačná. Záleží na definici nulové výšky (obvykle úroveň podlahy/země). Např. 0,5kg polštář může ze stejného okraje balkonu spadnout:
dovnitř balkonu (pak h\approx 1\,\mathrm m a E_\mathrm p\approx 5\,\mathrm J)
ven přes okraj a padat 4 patra dolů (pak dává smysl definovat nulovou výšku až na chodníku a tím pádem je h\approx 13\,\mathrm m s E_\mathrm p\approx 65\,\mathrm J).
Kinetická energie
Pro hmotný bod (nebo nerotující těleso) je úměrná druhé mocnině rychlosti:
E_\mathrm k=\frac{1}{2}mv^2
V klidu je tedy nulová. Protože se zvedá s druhou mocninou rychlosti, znamená to, že vůči rychlosti nejde o přímou úměru:
- rychlost v se zvýší na 2násobek → E_\mathrm k se zvýší na 2²násobek, tedy 4krát
- rychlost v se zvýší na 5násobek→ E_\mathrm k se zvýší na 5²násobek, tedy 25krát
- rychlost v klesne na 1/2 → E_\mathrm k klesne na 1/2²násobek, tedy na 1/4
Vůči hmotnosti ale o přímou úměru jde:
- hmotnost m se zvýší na 3násobek → E_\mathrm k vzroste na 3násobek
- hmotnost m klesne na 1/10 → E_\mathrm k klesne na 1/10
Takže jak se změní E_\mathrm k, když hmotnost klesne na třetinu, ale rychlost vzroste dvakrát? Musíme ji vynásobit součinem 1/3 krát 2². Tedy vzroste na \frac{4}{3}E_\mathrm k.
Kinetická energie balvanu
Balvan o m=10\,\mathrm{kg} se uvolnil a valí se z kopce.
- Na začátku má v=0\,\mathrm{m/s} proto je E_\mathrm k=0\,\mathrm J.
- Po chvíli se rozjede na v=2\,\mathrm{m/s} a má E_\mathrm k=\frac{1}{2}\cdot 10\cdot 2^2\,\mathrm J=20\,\mathrm J.
- Do údolí dorazí rychlostí v=4\,\mathrm{m/s} a tedy s kinetickou energií E_\mathrm k=\frac{1}{2}\cdot 10\cdot 4^2\,\mathrm J=80\,\mathrm J.
Když těleso rotuje má tato kinetická energie ještě jednu složku \frac{1}{2}J\omega^2, tou se zde ale nezabýváme, často ji totiž můžeme zanedbat.
NahoruMechanická energie tělesa a soustavy těles
Mechanická energie tělesa
Je rovna součtu kinetické a potenciální energie (E_\mathrm k a E_\mathrm p) tělesa. Značíme ji obvykle pouze jako E (pokud nepotřebujeme rozlišovat i jiné formy energie nebo další tělesa).
E=E_\mathrm k+E_\mathrm p
Mechanická energie parašutisty
Parašutista má v jednu chvíli E_\mathrm p=2400\,\mathrm J (vůči zemi) a E_\mathrm k=400\,\mathrm J
- Mechanická energie je E_\mathrm p+E_\mathrm k. Tedy 2400 J plus 400 J .
- Mechanická energie parašutisty je 2800 J.
Mechanická energie soustavy těles
Celkovou mechanickou energií soustavy těles je obyčejný součet mechanických energií jednotlivých těles. Mechanické energie jednotlivých těles píšeme s indexem tělesa (E_\mathrm {1}, E_\mathrm {2},…). Celkovou mechanickou energii pak bez indexu jen jako E.
E=E_\mathrm 1+E_\mathrm 2 +\cdots
Pokud rozepíšeme mechanické energie jednotlivých těles (např. E_1=E_\mathrm {k,1}+E_\mathrm {p,1}) může to vypadat také jako
E=E_\mathrm {k,1}+E_\mathrm {p,1}+E_\mathrm {k,2}+E_\mathrm {p,2}+\cdots
Mechanická energie akrobatů ve vzduchu
Jeden akrobat má mechanickou energii (součet svých E_\mathrm p+E_\mathrm k) rovnu 900 J. Druhý akrobat 1000 J a třetí 200 J.
- Celková mechanická energie soustavy je jejich součtem. Tedy 900+1000+200 J.
- Celková mechanická energie akrobatů je 2100 J.
Zákon zachování mechanické energie
Když se mechanická energie nepřeměňuje na jiné formy (např. na tepelnou energii třením), nebo když je tato přeměna zanedbatelná, můžeme použít zákon zachování mechanické energie (ZZME). Ten říká, že se mechanická energie v čase nemění (např. během pohybu, pružných srážek, …).
Jedno těleso
Pro jedno těleso to můžeme zapsat jako
E_\mathrm p+E_\mathrm k=\mathrm{konst.}
Takže o kolik se jedna složka energie zmenší, o to musí druhá vzrůst. Nejčastěji to můžeme využít u vrhů či pohybu tělesa po nakloněné rovině (bez tření).
Příklad: Padající tenisák
Tenisák o hmotnosti 0,1 kg upustíme z výšky 2 m na zem. Jaká je jeho kinetická energie 0,4 m nad zemí?
- Na začátku:
E_\mathrm p=mgh\approx 0{,}1\cdot 10\cdot 2\,\mathrm J=2\,\mathrm J
E_\mathrm k=\frac{1}{2}mv^2=0\,\mathrm J (nulová rychlost v)
celková mech. energie je tedy E=E_\mathrm k+E_\mathrm p=2\,\mathrm J
- 0,4 m and zemí:
E_\mathrm p=mgh\approx 0{,}1\cdot 10\cdot 0{,}4\,\mathrm J=0{,}4\,\mathrm J
Aby byl stále součet E_\mathrm k+E_\mathrm p roven 2 J, musela E_\mathrm k vzrůst o tolik, o kolik klesla E_\mathrm p. Tedy E_\mathrm k=1{,}6\,\mathrm J.
- Úpravou vzorce E_\mathrm k=\frac{1}{2}mv^2 bychom pak mohli vypočítat i rychlost (bez počítání rovnic volného pádu).
Příklad: Hod oštěpem
Jaké výšky mohl dosáhnout 1kg oštěp vržený E_\mathrm k=150\,\mathrm J pokud měl v nejvyšším bodě kinetickou energii jen E_\mathrm k=30\,\mathrm J?
- E_\mathrm p není zadaná, zřejmě je tedy na začátku hodu prakticky nulová.
- Snížení E_\mathrm k o 120 J musí podle E_\mathrm k+E_\mathrm p=\mathrm{konst.} znamenat E_\mathrm p=120\,\mathrm J.
- Z E_\mathrm p=mgh už snadno vyjádříme výšku h=\frac{E_\mathrm p}{mg}\approx\frac{120}{10}\,\mathrm m=12\,\mathrm m
Dvě a více těles
Pro izolované soustavy dvou a více těles platí, že se nemění celková mechanická energie. Například pro dvě tělesa to můžeme zapsat jako.
E_1+E_2=\mathrm{konst.}
nebo
E_\mathrm {p,1}+E_\mathrm {k,1}+E_\mathrm {p,2}+E_\mathrm {k,2}=\mathrm{konst.}
Mechanické energie jednotlivých těles se měnit mohou (např. po srážkách, vzájemným silovým působením). Setkáme se s ním u pružných srážek (např. kulečníkové koule) nebo pohybů vesmírných soustav.
Příklad: Kulečníkové koule
Jedna koule stojí. Druhá s kinetickou energií 2,5 J do ní narazí a zastaví se. Jakou kinetickou energii bude mít první koule?
- Všechny E_\mathrm p jsou stejné (vůči stolu nulové), můžeme je tedy z rovnic vynechat.
- Před srážkou: E_\mathrm {k,1}=0\,\mathrm J a E_\mathrm {k,2}=2{,}5\,\mathrm J. Takže E=E_\mathrm {k,1}+E_\mathrm {k,2}=2{,}5\,\mathrm J
- Po srážce: E_\mathrm {k,1}=? a E_\mathrm {k,2}=0\,\mathrm J
- Aby zůstal součet obou energií roven 2,5 J, musí být E_\mathrm {k,1} po srážce rovna právě 2,5 J.
Příklad: Kometa
Jak se změní rychlost komety při průletu kolem Slunce?
- I zde platí, že E_\mathrm p tělesa je tím menší, čím jsme blíž k zemi.
- Když se tedy kometa přibližuje ke Slunci její E_\mathrm p klesá (a E_\mathrm p Slunce také).
- Podle zákona zachování energie tedy musí vzrůst kinetické energie (Slunce i komety). A tedy i rychlost.
- Proto se rychlost komety při průletu kolem Slunce zvýší.
Práce (značíme W) je forma přenosu energie, proto má také stejnou jednotku, Joule.
V klasické mechanice se zabýváme především prací vykonanou působením síly na těleso po nějaké dráze. Práci ale koná jen ta část síly F, která je ve směru pohybu. Pro posun jedním směrem o s tedy můžeme psát:
W=F_\parallel\cdot s
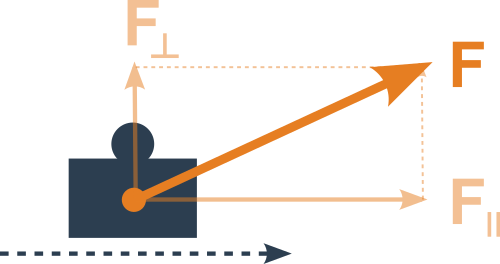
Pokud síla směřuje stejným směrem jako pohyb je to prostý součin W=F\cdot s
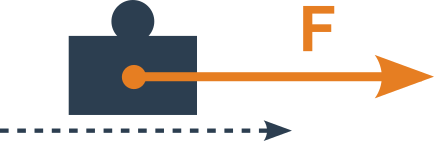
Pokud síla směřuje opačným směrem než pohyb, je práce záporná (W=-F\cdot s).

Pokud je síla kolmá na směr pohybu, je práce nulová.

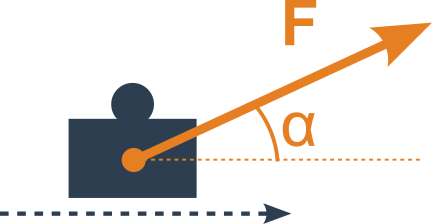
Zajímavosti
W=F\cdot s \cdot\cos\alpha
Výkon: základy
Veličina výkon v mechanice popisuje, jak rychle je konána práce W. Je definován doslova jako množství práce (W) za jednotku času (t). Značíme jej P, jeho jednotkou je watt (W).
Matematicky můžeme věty výše zapsat:
P=\frac{W}{t}
Ze vzorce výše můžeme odvodit i vztahy pro práci W=P\cdot t a čas t=\frac{W}{P}.
Čím větší je výkon, tím rychleji je práce konána (víc joulů práce za sekundu). U člověka odpovídá tomu, jak rychle se snažíme vykonat nějaký úkol, i když jej nemůžeme úplně ztotožnit s námahou (kvůli funkci kostry a svalů se namáháme i tehdy, když jen něco držíme a fyzikální práci prakticky nekonáme).
Protože se obvykle dozvíme jen množství práce za nějakou (delší) dobu, získáme takto průměrný výkon spíš než okamžitý.
Zde se procvičuje jen výkon spojený s mechanickou prací, existují ale formy spojené i s jinými přeměnami energie (elektrický výkon, tepelný výkon, …). Toho mechanického dokáže člověk snadno vyvinout i stovky wattů W. Vysavač třeba 1000 W. A auto třeba 100 kW.
Výkon tahače saní
Jaký průměrný výkon podal člověk který taháním saní vykonal práci 100 J za 20 s?
- Výkon je práce děleno čas.
- Tedy P=\frac{W}{t}
- Dosadíme práci 100 J a čas 20 s.
- Výkon byl tedy 5 W. (sáňky asi dobře klouzaly).
Výkon výtahu
Jaký výkon má výtah, který za 8 s vyveze 2kg náklad o 4 m nahoru?
- Když něco zvedáme, zvýší se polohová energie o E=mgh. Toto zvýšení energie odpovídá práci.
- Práce W je tedy rovna E=mgh\approx 2\cdot 10\cdot 4\,\mathrm J=80\,\mathrm J.
- Čas je 8 s.
- Dosadíme do P=\frac{W}{t}.
- Výkon byl tedy 80 děleno 8 wattů. Tedy 10 wattů.
Pokud za práci dosadíme práci nějaké tažné síly F na dráze s, dostaneme pro výkon nakonec vztah P=F\cdot v. Tomu se věnujeme v samostatném cvičení Výkon síly konající práci.
NahoruVýkon síly konající práci
Pokud je výkon P je roven práci W dělené časem t. Můžeme ale za práci dosadit konkrétně. Třeba práci síly během pohybu po určité dráze, tedy W=F_\parallel \cdot s. (pro další text předpokládejme, že je síla F leží ve směru pohybu, tedy místo F_\parallel \cdot s budeme psát přímo F\cdot s).
Dosadíme do P=\frac{W}{t}:
P=\frac{F\cdot s}{t}
Jenže s/t (dráha za čas) je definice rychlosti v. Proto je výkon takové síly roven:
P=F\cdot v
Tedy výkon je součinem síly pohonu a rychlosti. Může být jinak značena (např F_1, F_\mathrm{motoru}, …). Nejde tedy automaticky o výslednici sil.
- Autíčko je poháněno vpřed silou 20 N a jede 2 m/s . Výkon pohonu je 20 krát 2 wattů. Tedy 40 W.
- Saně táhneme vpřed silou 15 N, brzdí nás tření 10 N a jdeme rychlostí 1 m/s . Výkon tažné síly je 15 krát 1 wattů (odporová síla nás nezajímá). Tedy 15 W.
Tento vzorec snadno upravíme na vzorce pro velikost síly F=\frac{P}{v} nebo rychlosti v=\frac{P}{F}.
- Cyklista dává do šlapátek výkon 100 W a jede rychlostí 10 m/s. Podle F=\frac{P}{v} tedy pohání kolo silou 100/10 newtonů. Tedy 10 N.
Zajímavější jsou ale jeho důsledky. Například spousta motorů má konstantní výkon (nebo konstantní maximální výkon). Podle P=F\cdot v musí být pak konstantní i součin F\cdot v. Takže při zvýšení rychlosti bude hnací síla motoru se stálým výkonem klesat. Třeba i do té míry, že odporové síly pohybu se jí vyrovnají a výslednice sil bude nulová, nebo dokonce bude mít opačný směr.
Druhá výhoda vztahu P=F\cdot v je, že pokud dosadíme okamžitou rychlost v dostáváme jako výsledek okamžitý výkon. To s prací obvykle uváděnou za nějakou dobu a časovým intervalem nešlo (získávali jsme jen průměrný výkon za tento čas).
NahoruÚčinnost a příkon
Účinnost je číslo od 0 do 1 (popř. od 0 % do 100 %), které vyjadřuje, jakou část dodávaného výkonu dokáže spotřebič využít k vykonávání své funkce. Skutečná účinnost nemůže být vyšší než 100 % (takové zařízení by vyrábělo energii z ničeho – perpetuum mobile).
Účinnost značíme řeckým písmenem η (éta). Je bezrozměrná (jednotkou je 1).
Dodaný výkon označujeme jako příkon a značíme P_0. Využitý výkon označujeme prostě jako výkon (spotřebiče) a značíme P.
Matematicky zapíšeme účinnost jako \eta = \frac{P}{P_0}.
Úpravou odvodíme také vztahy pro výpočty výkonu P=\eta\cdot P_0 a příkonu P_0 = \frac{P}{\eta}.

Příklad: žárovka
- Žárovka odebírá ze zásuvky příkon 80 W. Na očekávanou světelnou energii se přemění ale jen 12 W.
- Zbytek výkonu se přemění hlavně na teplo, ale kvůli topení žárovku nepoužíváme.
- Účinnost tedy je jen \eta=12/80=0{,}15= 15\,\%.
Příklad: rychlovarná konvice
- Rychlovarná konvice odebírá 2000 W. Skoro všechnu energii přeměňuje na teplo, ale jen 1900 W tepelného výkonu ohřívá vodu.
- Zbytek tepelného výkonu ohřívá např. konstrukci konvice, nebo okolní vzduch (což nepotřebujeme). Malá část příkonu je navíc přeměněna na elektromagnetickou energii.
- Účinnost tedy je \eta=1900/2000=0{,}95= 95\,\%.
Zajímavosti
Některé stroje se chlubí účinností přes 100 % (např. kondenzační kotel). Ale nebojte, fyzikální zákony stále platí – energie se nedá vyrobit z ničeho. Hodnota přes 100 % je způsobena prostě tím, že výrobce do příkonu P_0 nezapočítal veškerou energii obsaženou v palivu, ale jen jeho tzv. výhřevnost. Energii ve spalinách (kterou kondenzační kotle umí využít) zkrátka přehlíží.

