I z grafů dráhy/polohy můžeme určit rychlost a z grafů rychlosti dráhu. Ne vždy je to jednoduché udělat přesně, ale alespoň odhadnout je můžeme vždy.
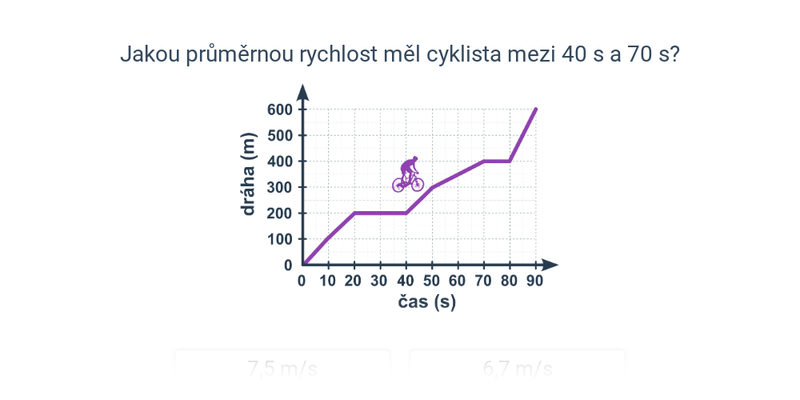
Výpočet rychlosti z grafu polohy/dráhy
Můžeme určovat průměrnou rychlost celého pohybu (v=s/t) nebo nějakého jeho úseku (v=\Delta s/ \Delta t). Symbol \Delta značí rozdíl hodnot, např. \Delta t = t_\mathrm{konec}-t_\mathrm{zacatek}.
Odečteme údaje na osách pro oba krajní body úseku a dosadíme do výpočtu:
v=\frac{s_\mathrm{konec}-s_\mathrm{zacatek}}{t_\mathrm{konec}-t_\mathrm{zacatek}}
Příklad: Celková průměrná rychlost pohybu se změnou rychlosti
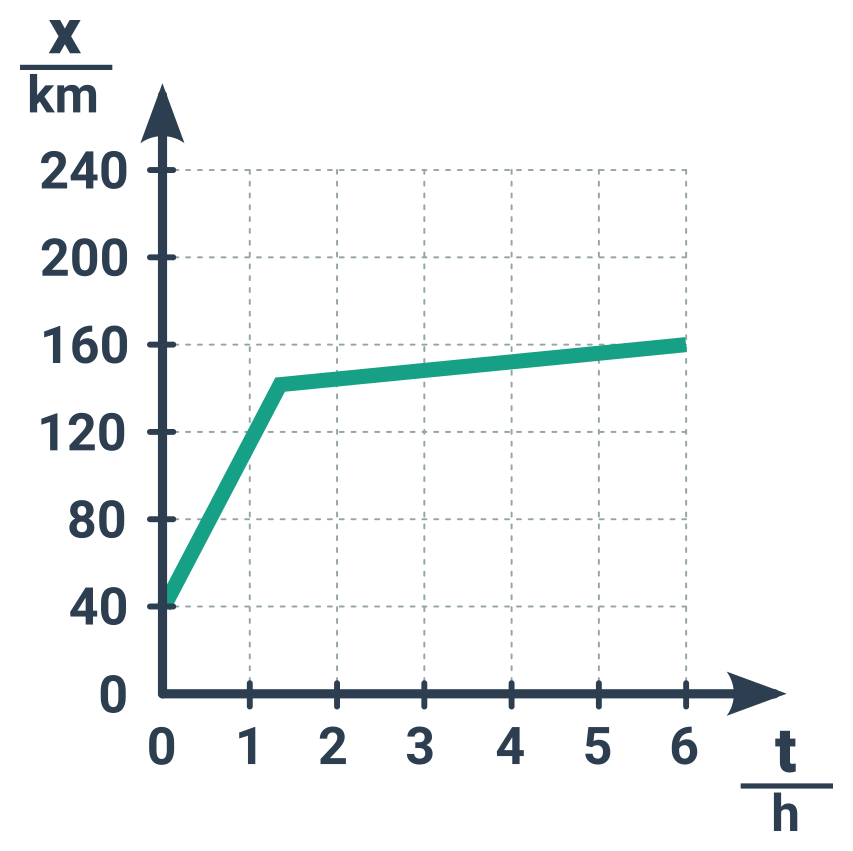
Dosadíme krajní hodnoty do vzorce (160 km a 40 km do čitatele, 6 h a 0 h do jmenovatele) a dostaneme průměrnou rychlost

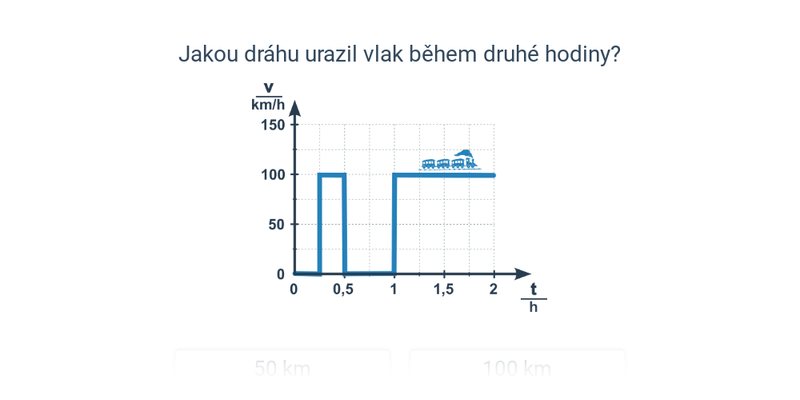
Výpočet dráhy z grafu rychlosti
V grafu rychlosti tělesa je dráha vlastně obsahem plochy pod křivkou rychlosti. Obecně je to těžké. Někdy jsou ale pod křivkou jednoduché tvary, jejichž obsah známe. Jindy obsah můžeme alespoň přibližně odhadnout.
Obdélníky:
Obsah obdélníka je strana krát strana, zde tedy vlastně s=v\cdot t.
Příklad: Dráha cyklisty
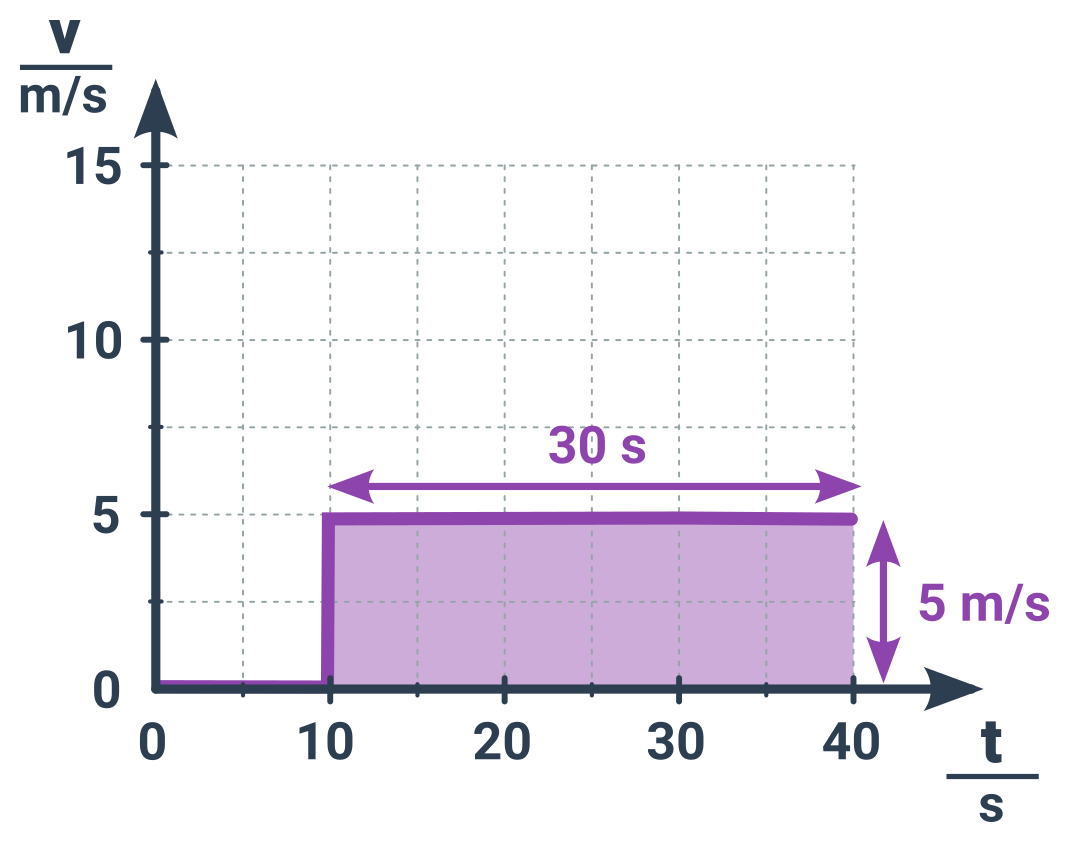
Oblast pod křivkou je obdélník, když jeho rozměry vynásobíme dostaneme ihned výslednou dráhu.

Pozn.: Pravoúhlý trojúhelník má obsah jako polovina obdélníka.
Postup použitelný i pro složitější tvary (minimálně odhad) využívá mřížky grafu. Spočítáme obsah jednoho čtverce mřížky a pak vynásobíme počtem čtverců pod křivkou (nemusí být celé číslo).
Příklad: Dráha cyklisty pomocí mřížky
Z grafu
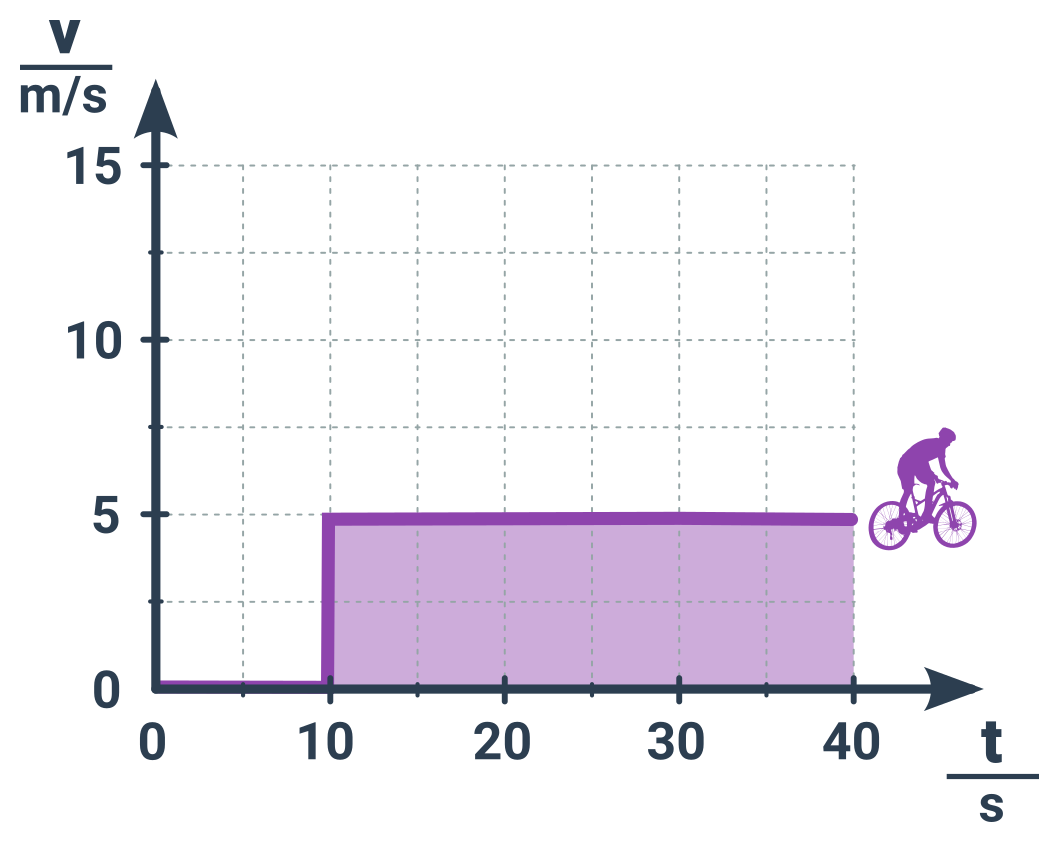
určíme obsah jednoho čtverce mřížky

Pod křivkou je 12 takových čtverců, takže

Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.