Výpis souhrnů
Grafy pohybu
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Grafy pohybu
Grafy pohybu jsou nejčastěji 2-D grafy, jak je známe z matematiky, které zobrazují vývoj nějaké veličiny popisující pohyb (y-ová, svislá osa) v závislosti na čase (x-ová, vodorovná osa).
Zobrazované veličiny jsou typicky poloha (na trati nebo dráze, obvykle nejde o skutečnou 3-D polohu), uražená dráha, nebo rychlost. Ale mohli bychom zobrazovat i např. zrychlení nebo jiné, obskurnější veličiny. Jde vlastně o záznam „měření“ dané veličiny v čase.
Z grafu pohybu můžeme:
- Zjistit typ grafu, o který se jedná (zaznamenaná veličina, počet těles, …).
- Získat základní informace o pohybu podle tvaru křivky v grafech. Jak v grafech polohy/dráhy, tak rychlosti.
- Odečítat hodnoty v grafech polohy i rychlosti v konkrétních bodech pohybu (např. v jakém čase byla rychlost nejvyšší).
- Vypočítat další veličiny (například rychlost z grafu dráhy nebo dráhu z grafu rychlosti).
Typy grafů pohybu
Rozlišujeme dva nejčastější typy grafů. Ty které zobrazují prostorovou veličinu (poloha, dráha) a ty které zobrazují rychlost. Poznáme to podle toho jak je označena svislá osa grafu. Kromě toho mohou existovat graf i jiných veličin (např. zrychlení), ale většinou je nepoužíváme.
Přitom jeden graf může zachycovat pohyb jednoho, ale i více těles (pak se v něm nachází více křivek, nebo sad bodů).
NahoruGrafy polohy/dráhy: základy
Grafy polohy (zde značíme x) a uražené dráhy (zde značíme s) jsou často vzájemně zaměnitelné, někdy ale ne. Dráha totiž narůstá i když se otočíme a začneme se po trase vracet. Poloha ne. Dráha navíc obvykle začíná na nule, což poloha nemusí. Ilustrují to následující grafy stejného pohybu dvou těles – jednou pro polohu, podruhé pro dráhu.
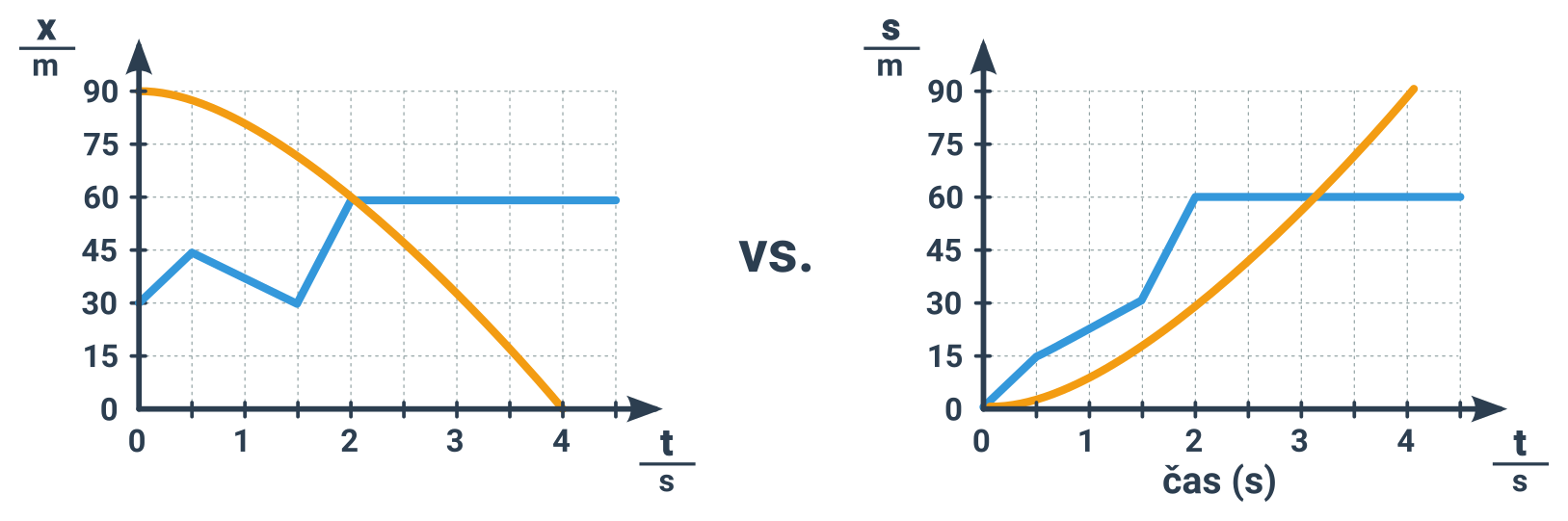
Platí, že čím strmější je křivka, tím rychlejší je pohyb. To znamená několik základních pouček pro kvalitativní pochopení zobrazeného pohybu:
- zlom křivky = náhlá změna rychlosti
- ohýbání křivky = plynulá změna rychlosti
- přímé úseky = rovnoměrný pohyb
- vodorovná část křivky = těleso stojí na místě
Příklad: Dráha auta a cyklisty
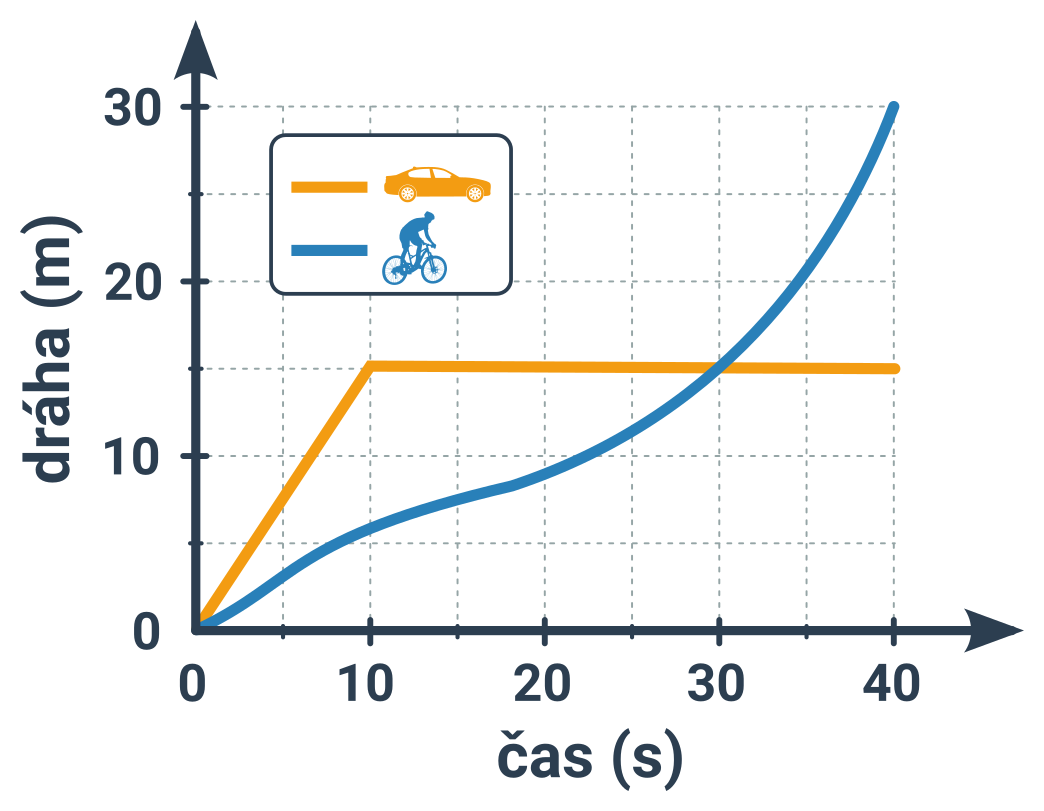
- Podle legendy je auto znázorněno oranžovou křivkou.
- Ta zpočátku (pravý kraj grafu) stoupá, auto se tedy pohybuje (dráha roste). A protože je tento úsek úsečka (nezakřivená), pohyb auta je tu rovnoměrný.
- Poté se křivka náhle zlomí do vodorovna. Auto tedy v mžiku změnilo rychlost na nulovou a stojí na místě. Až do konce (křivka je vodorovná až do konce grafu).
- Modrá křivka cyklisty je stále skloněná. Cyklista se tedy celou dobu pohybuje. Sklon se ale mění (nejde o úsečku). Jeho pohyb je tedy nerovnoměrný.
- Nejstrmější je křivka na konci, tehdy má tedy cyklista nejvyšší rychlost.
Grafy polohy/dráhy: odečítání údajů
Pro odečítání nějaké hodnoty z grafu existuje několik základních úkolů:
1. Máme daný bod na křivce a máme zjistit jeho souřadnici (časovou nebo polohovou/dráhovou).
Jednoduše z tohoto bodu vedeme kolmici na osu žádané veličiny. Poloha průsečíku pak odpovídá hledané hodnotě.
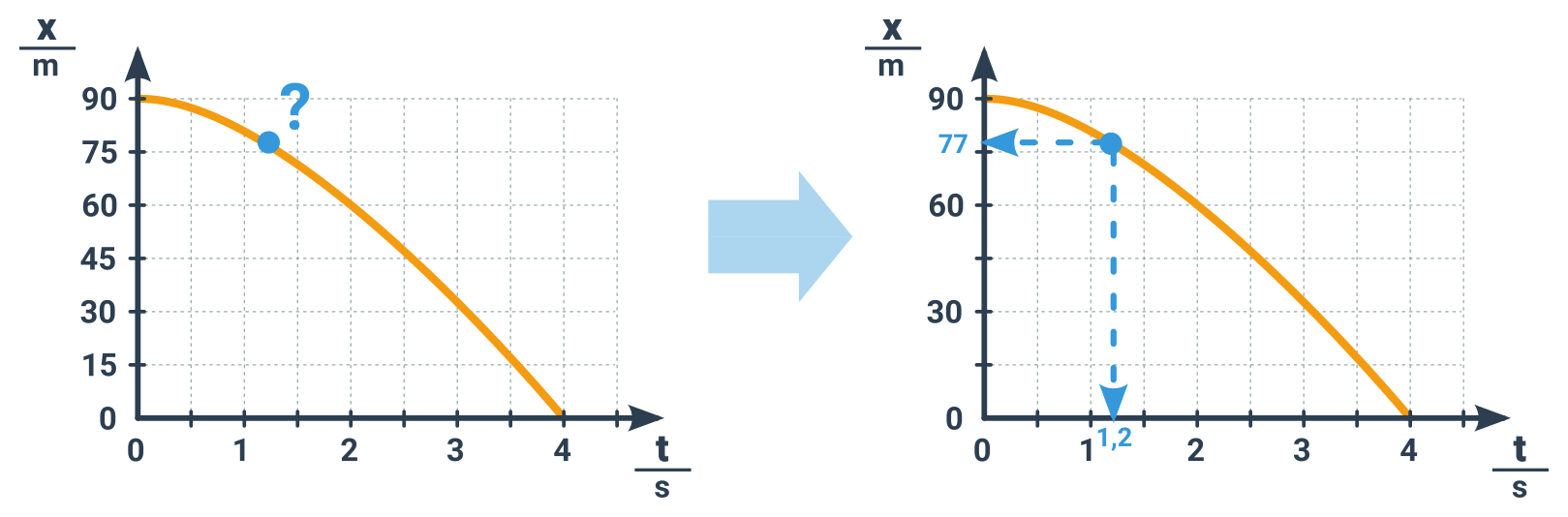
Nejčastěji když má samotný bod křivky nějaký význam, například zastavení tělesa (křivka se tam láme do vodorovna). Často jej tedy musíme nejprve identifikovat (můžete procvičit i zde)
Příklad: Poloha na konci
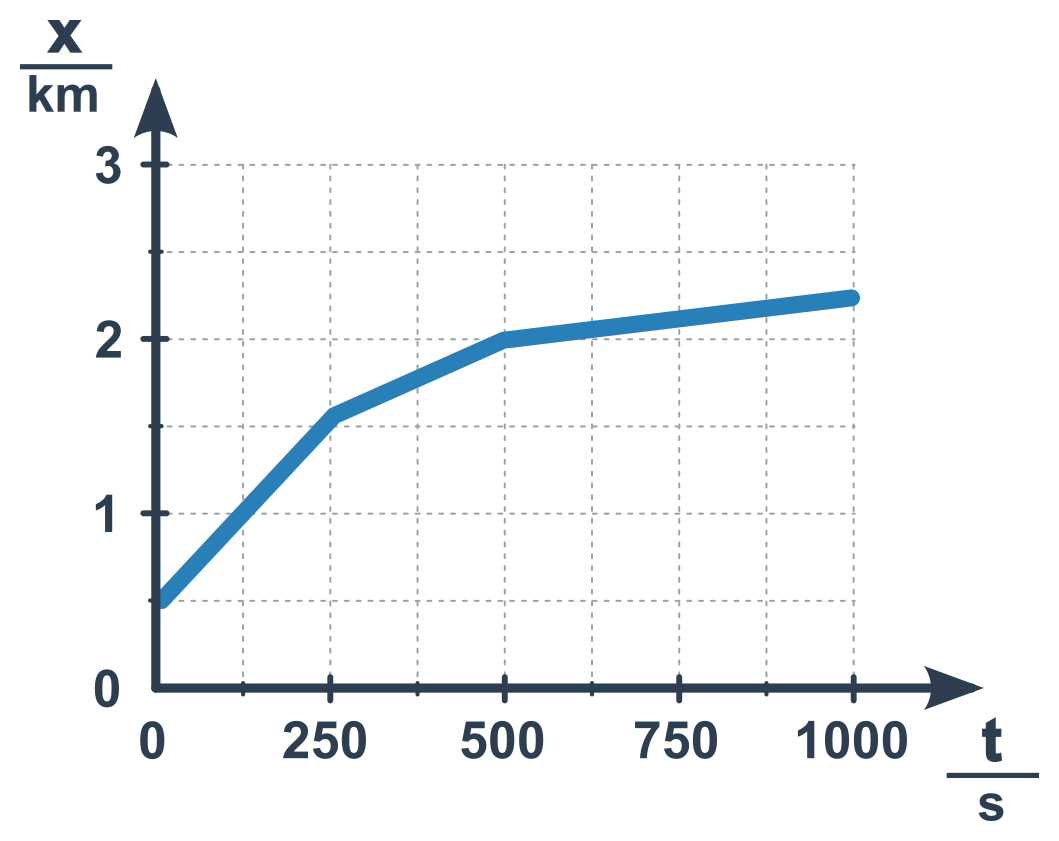
- Jakou polohu má těleso na konci sledování pohybu.
- Zjevně jde o bod na pravém konci křivky.
- Z tohoto bodu jedeme vodorovně doleva ke svislé ose.
- Protneme ji asi půl dílku nad 2. Velikost dílku je 0,5 km.
- Proto je poloha tělesa na konci 2 plus polovina z 0,5. Tedy 2,25 km.
2. Pro daný čas hledáme polohu/dráhu tělesa.
Vedeme z tohoto časového bodu kolmici. Hledáme průsečík s křivkou pohybu. Z něj vedeme kolmici na osu polohy podobně jako v bodu 1.
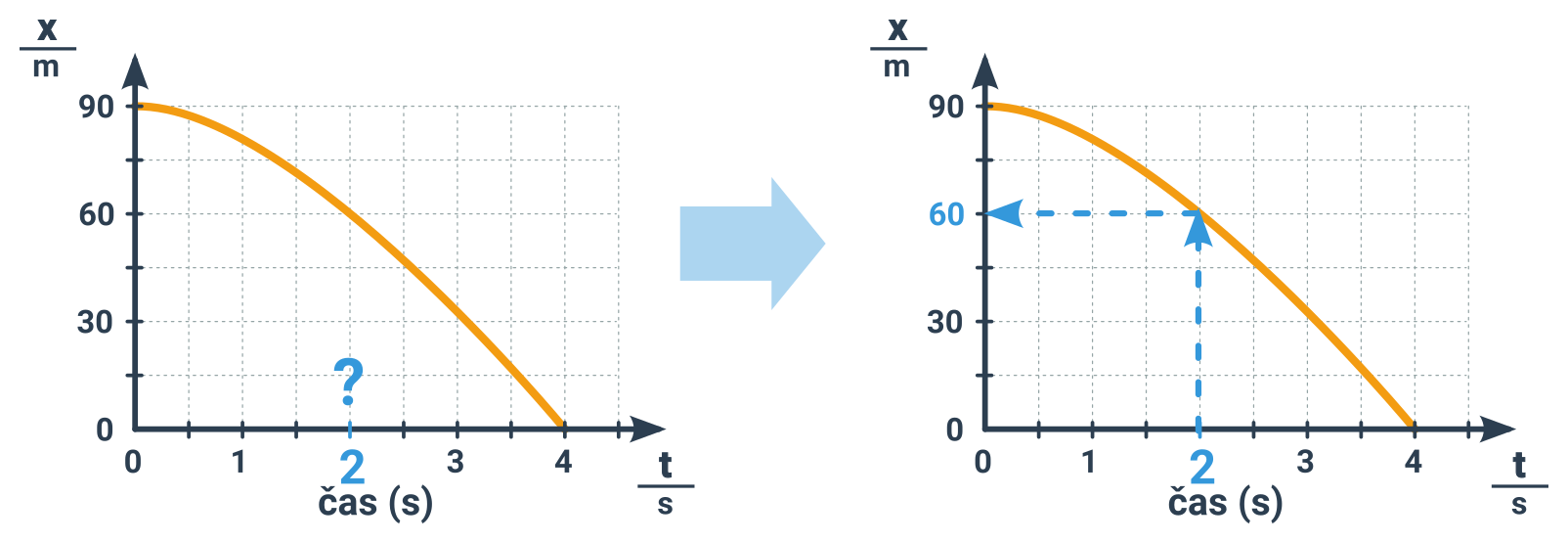
3. Pro určitou polohu/dráhu hledáme čas, kdy se na ni těleso nachází.
Postup je obdobný jako v bodě 2, jen začínáme ze svislé osy.
Ne vždy ale existuje řešení (průsečík s křivkou). Pak můžeme říct, že taková situace nenastane nikdy.
Příklad: Určení času při dosažení polohy 2 km

- Chceme znát čas, kdy je těleso na poloze 2 km.
- Najdeme na svislé ose 2 km a vedeme z ní vodorovnou čáru (zde už je naznačena mřížkou).
- Tam, kde se protne s křivkou pohybu, je náš bod. Je to přesně ve druhém zlomu křivky.
- Kolmo dolů pod tímto bodem dojdeme na časovou osu, na hodnotu 500 s.
Grafy rychlosti: základy
Grafy rychlosti zobrazují velikost rychlosti v čase. Nenesou informaci o poloze, byť uraženou dráhu z nich zjistit můžeme (čím větší plocha pod křivkou, tím větší uražená dráha). Z tvaru a polohy křivky můžeme určit některé kvalitativní vlastnosti pohybu:
- vodorovná část křivky na nule = těleso stojí na místě
- vodorovná část křivky = rovnoměrný pohyb
- přímé úseky (šikmo) = rovnoměrně zrychlený/zpomalený pohyb
- zakřivené úseky = nerovnoměrně zrychlený/zpomalený pohyb
Grafy rychlosti: odečítání údajů
Pro odečítání z grafů rychlosti platí to stejné jako pro odečítání údajů z grafů polohy a dráhy. Jen na svislé ose odečítáme rychlosti.
Řešíme tedy stejné tři úlohy – hledáme buď souřadnice bodu (který často musíme identifikovat), hodnotu rychlosti v daném čase, nebo čas, kdy má rychlost určitou hodnotu.
NahoruVýpočty rychlosti a dráhy z grafů
I z grafů dráhy/polohy můžeme určit rychlost a z grafů rychlosti dráhu. Ne vždy je to jednoduché udělat přesně, ale alespoň odhadnout je můžeme vždy.
Výpočet rychlosti z grafu polohy/dráhy
Můžeme určovat průměrnou rychlost celého pohybu (v=s/t) nebo nějakého jeho úseku (v=\Delta s/ \Delta t). Symbol \Delta značí rozdíl hodnot, např. \Delta t = t_\mathrm{konec}-t_\mathrm{zacatek}.
Odečteme údaje na osách pro oba krajní body úseku a dosadíme do výpočtu:
v=\frac{s_\mathrm{konec}-s_\mathrm{zacatek}}{t_\mathrm{konec}-t_\mathrm{zacatek}}
Příklad: Celková průměrná rychlost pohybu se změnou rychlosti
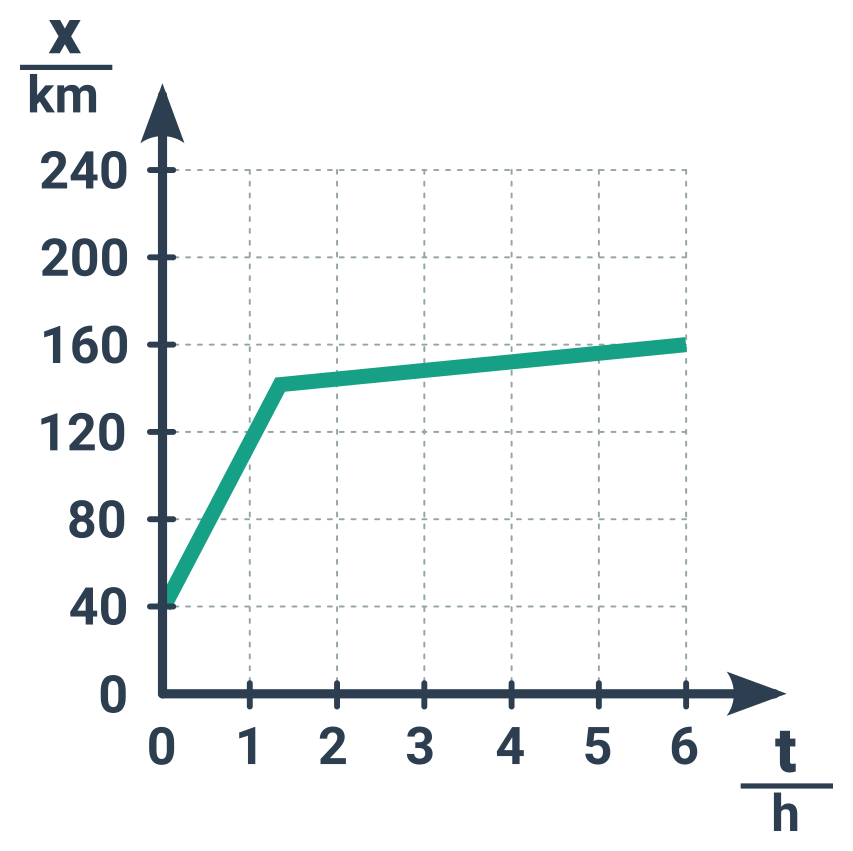
Dosadíme krajní hodnoty do vzorce (160 km a 40 km do čitatele, 6 h a 0 h do jmenovatele) a dostaneme průměrnou rychlost

Výpočet dráhy z grafu rychlosti
V grafu rychlosti tělesa je dráha vlastně obsahem plochy pod křivkou rychlosti. Obecně je to těžké. Někdy jsou ale pod křivkou jednoduché tvary, jejichž obsah známe. Jindy obsah můžeme alespoň přibližně odhadnout.
Obdélníky:
Obsah obdélníka je strana krát strana, zde tedy vlastně s=v\cdot t.
Příklad: Dráha cyklisty
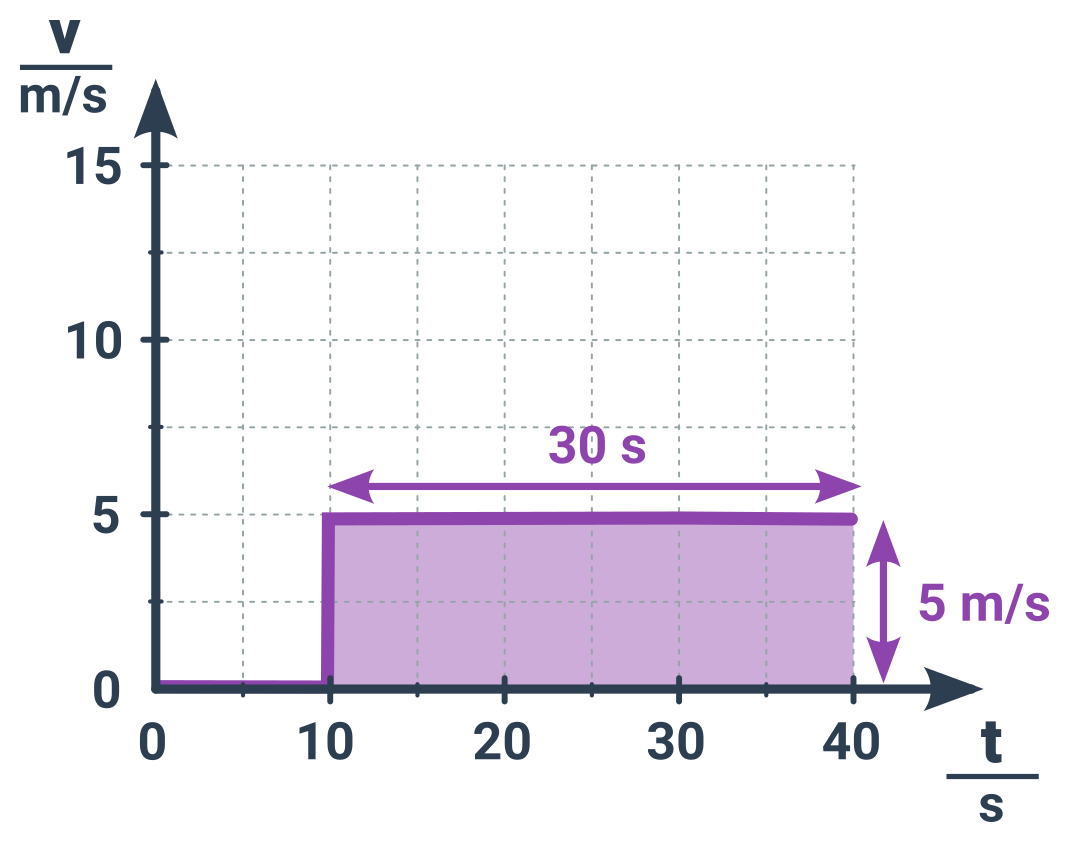
Oblast pod křivkou je obdélník, když jeho rozměry vynásobíme dostaneme ihned výslednou dráhu.

Pozn.: Pravoúhlý trojúhelník má obsah jako polovina obdélníka.
Postup použitelný i pro složitější tvary (minimálně odhad) využívá mřížky grafu. Spočítáme obsah jednoho čtverce mřížky a pak vynásobíme počtem čtverců pod křivkou (nemusí být celé číslo).
Příklad: Dráha cyklisty pomocí mřížky
Z grafu
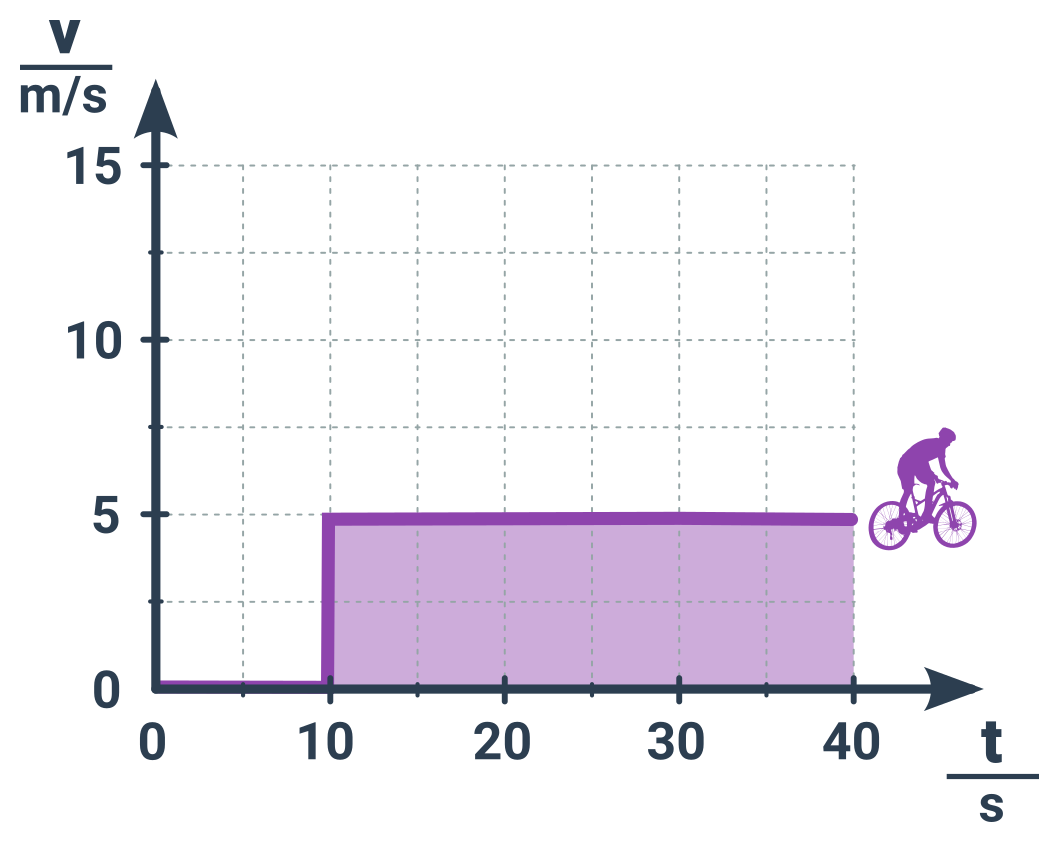
určíme obsah jednoho čtverce mřížky

Pod křivkou je 12 takových čtverců, takže


