Děkujeme za Vaše hodnocení.

Struktura pevných látek

2DH

umime.to/2DH

Podle struktury můžeme rozdělit pevné látky na krystalické (pravidelná struktura), amorfní (nepravidelná struktura) a polykrystalické. Na struktuře záleží i to jestli se látka chová ve všech směrech stejně. Taková látka je izotropní. Pokud tomu tak není (například kusy slídy se dobře lámou pouze v určitém směru), říkáme, že je látka anizotropní.

Krystalické látky

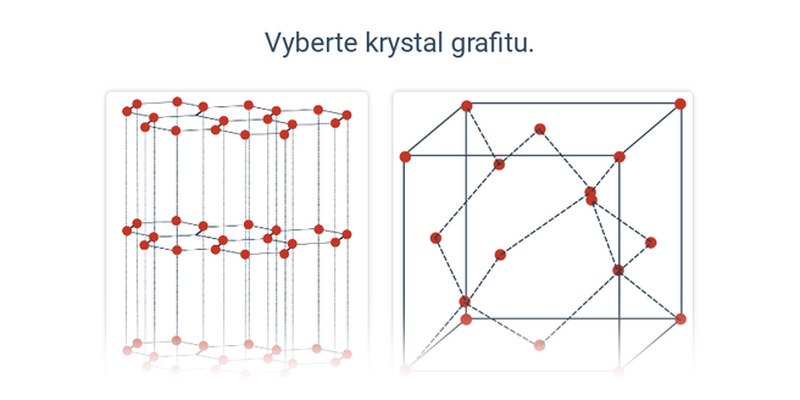
Částice jsou pravidelně rozmístěny v tzv. krystalové mřížce. Obecně mohou být anizotropní. Jde třeba o diamant, tuhu, krystalky síry, nebo led.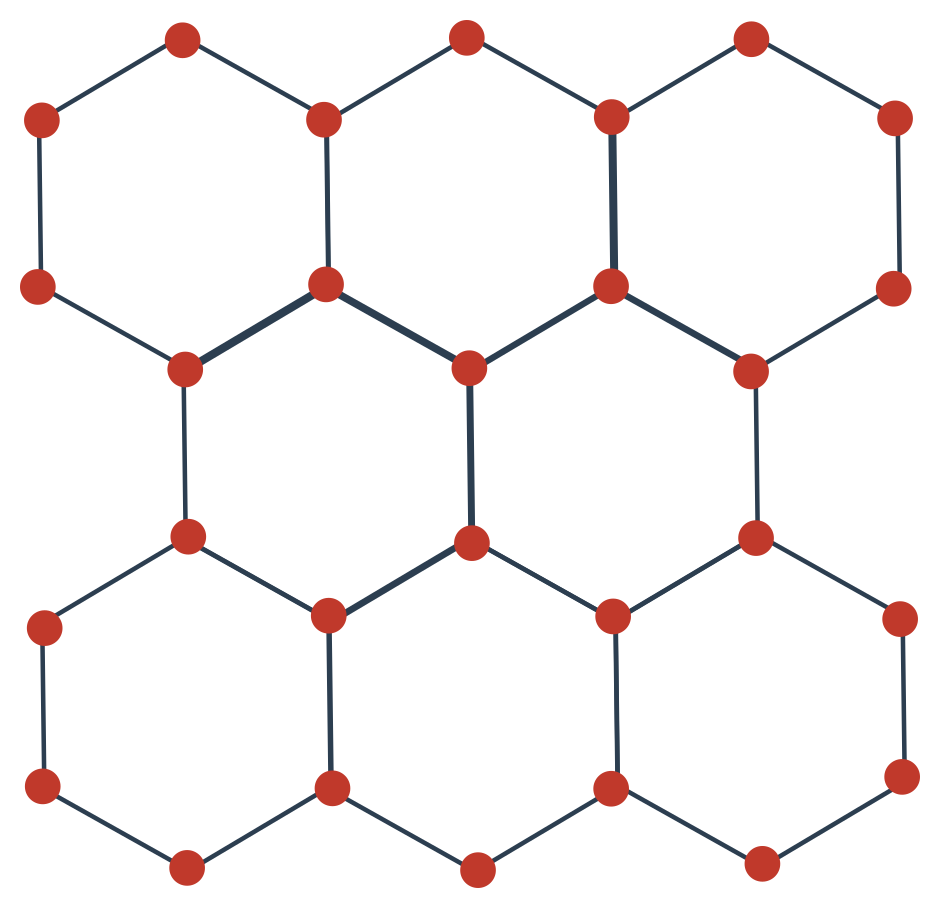

Amorfní látky

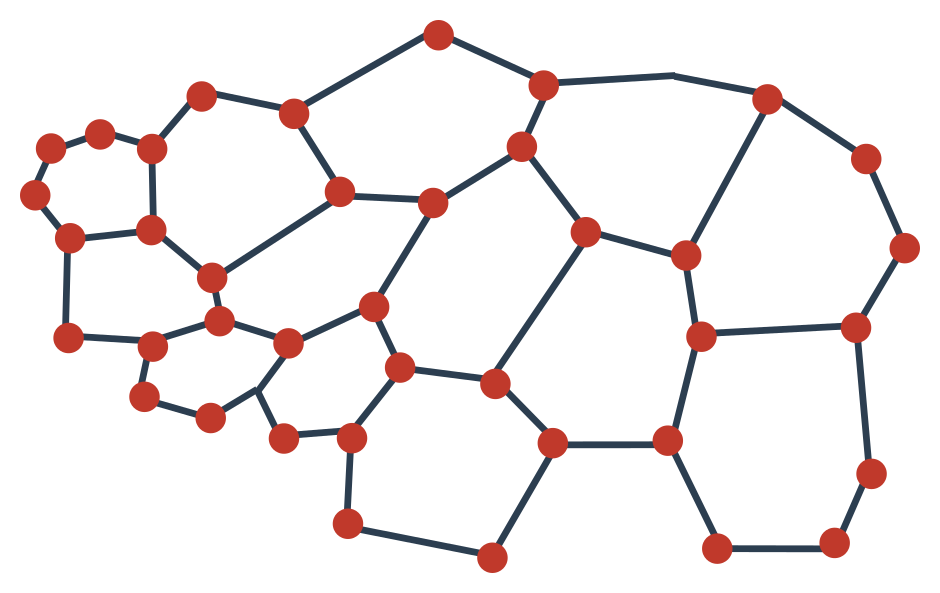
Částice nejsou v prostoru nijak uspořádány. Rozmístění je náhodné. I proto se látka vždy chová izotropně. Například jde o umělé látky, vosky nebo sklo.

Polykrystalické látky

Jde o takový hybrid mezi předchozími. Mnoho malých pravidelných zrn (krystalků) naskládaných a natočených náhodně. Patří sem všechny kovy.

Základní typy krystalové mřížky

Nejmenším celkem mřížky je elementární buňka. Může mít různý tvar (podle toho rozlišujeme různé krystalické soustavy) a taky různé rozmístění částic. Prostá buňka mřížky je tvořena jen částicemi v jejích rozích. Pokud mřížku tvoří prostorově centrované buňky, obsahují navíc jednu částici uprostřed. Plošně centrovaná buňka má navíc částici ve středu každé své stěny. Nejlépe je to vidět na krychlové mřížce:

prostá
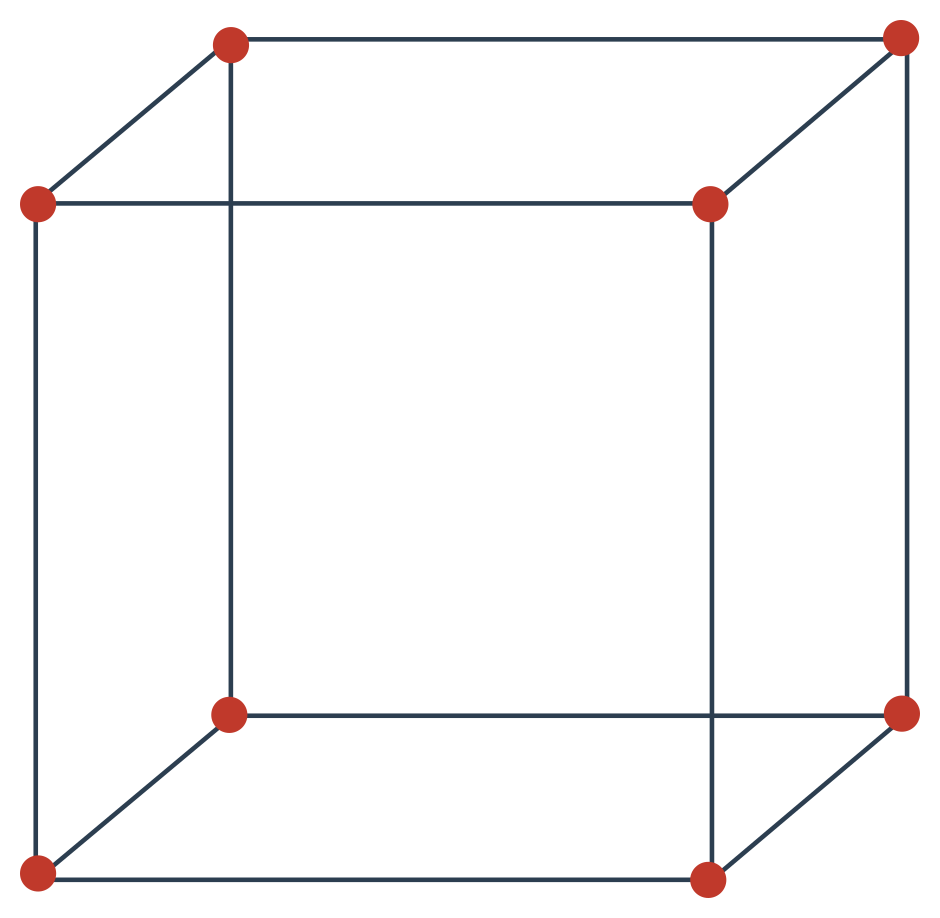
prostorově centrovaná
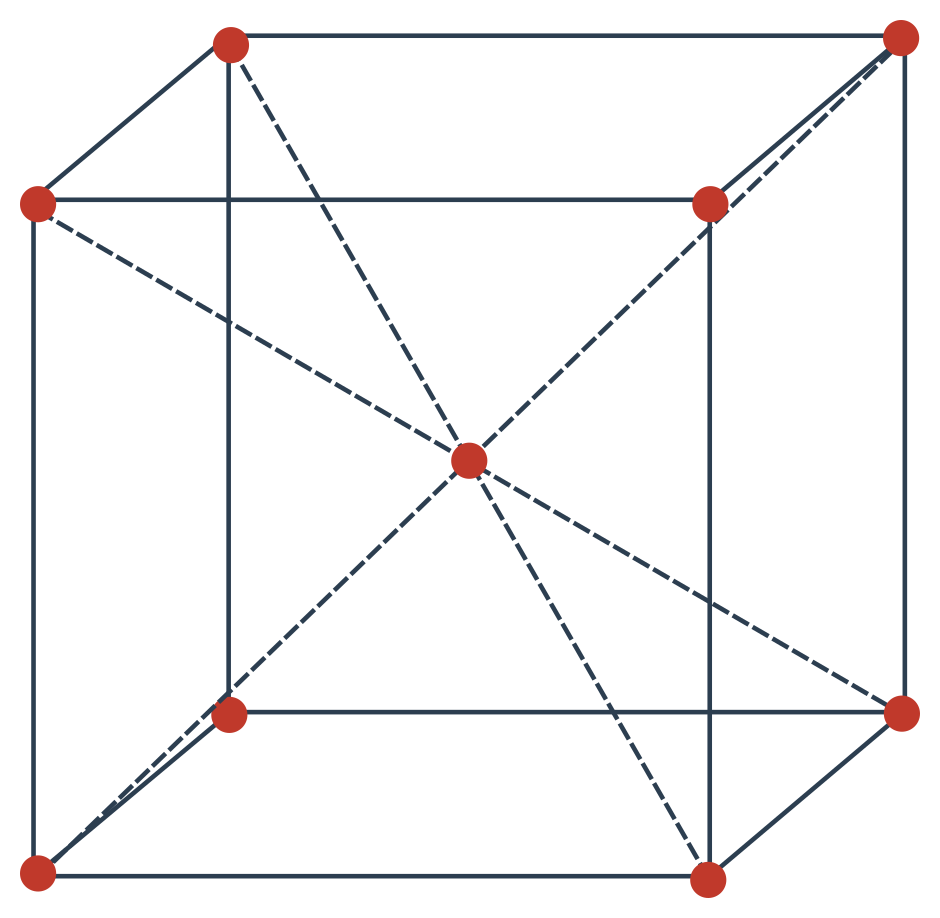
plošně centrovaná

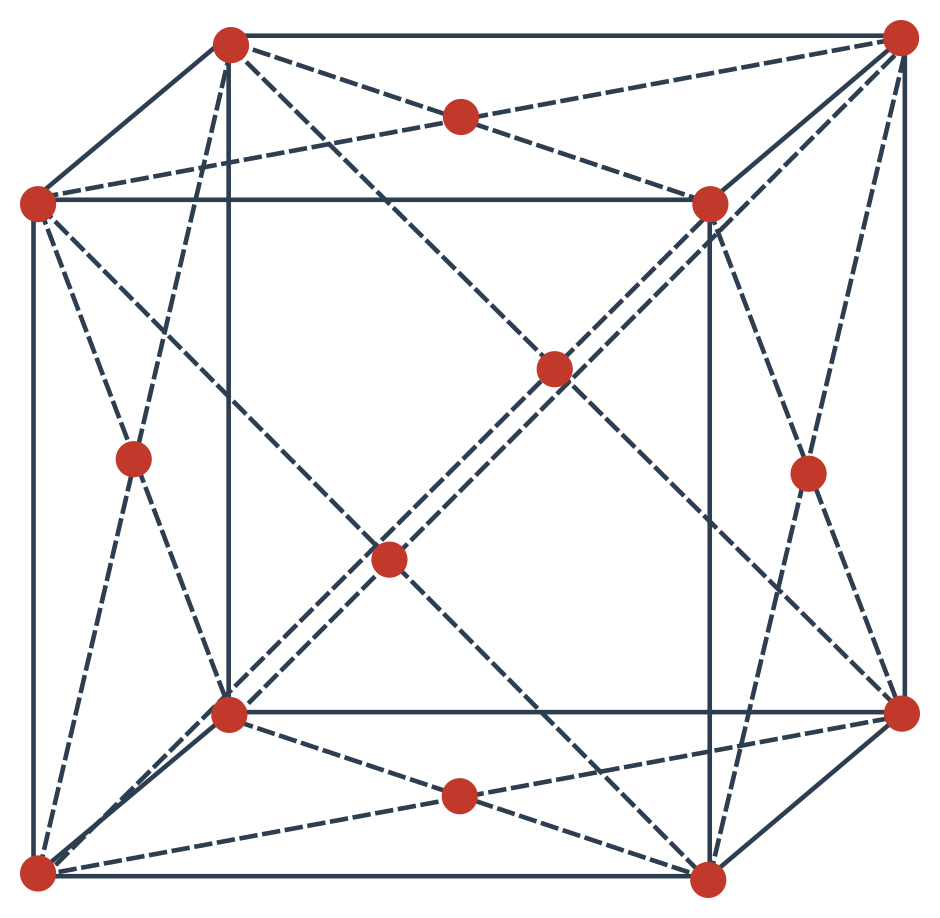
Počet částic připadající na jednu buňku

Můžeme spočítat počet částic připadající na jednu buňku.
Prostá: Každou částici sdíli osm buněk, jedna buňka se skládá z osmi částic, potom: \frac{1}{8}\cdot 8 = 1. Na jednu prostou buňku připadá jedna částice.
Prostorově centrovaná: Stejné jako u prosté buňky plus jedna částice uvnitř, která celá připadá této buňce, proto: \frac{1}{8}\cdot 8 + 1 = 2. Na jednu prostorově centrovanou buňku připadají dvě částice.
Plošně centrovaná: Stejné jako u prosté buňky plus šest částic ve stěnách, z nichž každá připadá dvěma buňkám, proto: \frac{1}{8}\cdot 8 + \frac{1}{2}\cdot 6 = 4. Na jednu plošně centrovanou buňku připadají čtyři částice.

Mřížkový parametr

Udává základní rozměr buňky. Většinou je to velikost hrany krychle/kvádru. Rozměrově bývá v jednotkách Ångstromů.

Hustota látky

ze znalosti mřížkového parametru a typu buňky lze spočítat hustotu látky
hustota je dána \varrho = \frac{m}{V}
hmotnost spočítáme jako m = N\cdot m_i (N – počet částic na jednu buňku, m_i – hmotnost jedné částice)
objem V = a^3 (objem krychle)
výsledná hustota \varrho = \frac{N\cdot m_i}{a^3}.

Ångstrom?

V atomární fyzice i v dalších partiích se můžete setkat se zvláštními jednotkami označovanými A s kroužkem: Å. Metry jsou pro tento způsob využití příliš velké. Základní převodním vztahem je: 1 nm = 10 Å

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Struktura pevných látek

Rozhodovačka • lehké

Cvičení

Struktura pevných látek

umime.to/2DH

Krystalické látky

Amorfní látky

Polykrystalické látky

Základní typy krystalové mřížky

Mřížkový parametr

Ångstrom?

Rozhodovačka