Výpis souhrnů
Elektřina a magnetismus
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
- Elektrický náboj
- Elektrické napětí
- Elektrická práce a výkon
- Elektrický proud v látkách
- Vodiče a izolanty
- Výpočet odporu vodiče
- Teplotní závislost odporu vodiče
- Ohmův zákon pro část obvodu
- Ohmův zákon pro celý obvod a zkrat
- Polovodiče
- Polovodiče: základy
- Polovodiče a proud
- Příměsi v polovodiči
- PN přechod
- Elektrostatika
- Coulombova síla ve vakuu
- Coulombova síla v látkách a permitivita
- Elektrické síly: více nábojů
- Střídavý proud
- Spojování rezistorů
- Spojování kondenzátorů
- Vzájemné působení magnetů
- Působení magnetů na látky
- Elektromagnetické jevy
- Elektromagnetická indukce
- Elektromagnetická indukce: základy
- Elektromagnetická indukce: vzorce a vztahy
- Lenzův zákon
Elektrický náboj
Elektrický náboj, je základní elektrická veličina. Označuje jednu ze základních vlastností látky – podobně jako hmotnost označuje jakou mají látky setrvačnost, nebo jak silně je přitahuje gravitace, popisuje náboj elektrické chování látky. Značíme jej q (nebo Q) a jeho jednotkou je coulomb (C). Měříme jej elektroskopem.
Na rozdíl od hmotnosti existují dva typy náboje – kladný (+) a záporný (−) náboj. Přitahují se vždy tělesa s opačným nábojem. Souhlasné náboje (např + a +) se odpuzují. Čím větší náboj, tím větší působení (elektrostatická síla), které ale se vzdáleností klesá.
Elektrický náboj tělesa se vlastně objevuje proto, že jej nesou různé elementární částice:
- elektrony mají jeden záporný náboj e^-
- protony mají jeden kladný náboj e
- neutrony mají nulový náboj (jsou neutrální a elektricky netečné)
Přitom e je tzv. elementární náboj – nejmenší možná hodnota náboje.
Látky se skládají z atomů a atomy se skládají z těchto částic. Jádro atomu tvoří protony a neutrony a obal je z elektronů. Pokud je součet kladných a záporných nábojů stejný, je atom (nebo molekula) elektricky neutrální. Pokud obsahuje jednoho náboje více jde o elektricky nabitou částici – iont (kladný = kationt, záporný = aniont). Také elektrony mohou existovat samostatně (a přecházet z jednoho těles na druhé).
Pokud tedy obsahuje těleso takové ionty (a součet jejich nábojů není 0), je těleso elektricky nabité. To je spíš výjimka (většina látek a těles kolem nás je elektricky neutrální).
NahoruElektrické napětí
Elektrické napětí je veličina odpovídající silám, které pohání tok elektřiny (elektrický proud). Jeho značka je U a jednotka volt (V). Napětí můžeme definovat pomocí práce vykonané W zdrojem (elektrickým polem) na přenesení náboje Q náboje. Je to jejich podíl:
U=\frac{W}{Q}.
Příklad: Napětí baterie
Síly v baterii postupně přenesly náboj 10 coulombů skrz žárovku a vykonaly při tom práci 125 joulů. Jaké má baterie napětí?
- Náboj Q je 10 C a práce W je 125 J.
- Můžeme dosadit do U=\frac{W}{Q}.
- U=\frac{125}{10}\,\mathrm V=12{,}5\,\mathrm V
- Napětí baterie je 12,5 V.
Platí tedy také vztahy W=Q\cdot U a Q=\frac{W}{U}.
Příklad: Práce vykonaná zdrojem
Motor pohání 9V baterie. Jakou práci musí vykonat pokud má motorem protéct náboj 200 C?
- Náboj Q je 200 C a napětí U je 9 V.
- Můžeme dosadit do W=Q\cdot U.
- W=200\cdot 9\,\mathrm J=1800\,\mathrm J
- Vykonaná elektrická práce baterie je 1800 joulů.
Jak si můžeme napětí intuitivně představit?
Můžeme si také představovat napětí jako rozdíl hladin vody v přehradě a pod přehradou. Pokud budou hladiny vyrovnané (napětí nula), voda neteče (proud neteče). Čím je rozdíl hladin (napětí) vyšší, tím větší tok vody (větší proud) může způsobit.
Napětí mezi dvěma body v obvodu měříme voltmetrem (popřípadě multimetrem nastaveným na voltmetr), který do obvodu připojujeme paralelně.
Zdroje napětí mají dva póly které určují směr toku proudu – kladný (+) a záporný (−). Tomu říkáme polarizace zdroje. Kolem sebe se setkáme různými zdroji napětí – chemickými (baterie a akumulátory), nebo těmi, kde jej na začátku vytváří z mechanické energie nějaký generátor:
- Voltův článek – historicky první baterie, stejnosměrné napětí
- AA baterie – 1,5 V, stejnosměrné napětí
- akumulátory – dobíjecí varianta „baterie“
- zásuvka doma – 230 V, póly ve zdířkách se vyměňují (střídavé napětí)
- svetr třený o vlasy – 10 000 V, stejnosměrné napětí
- dráty vysokého napětí – např. 22 000 V, polarizace drátu se střídá (střídavé napětí)
Z napětí svetru je také vidět, že velikost napětí, není úplně rozhodující pokud jde o nebezpečnost. Nebezpečné je totiž hlavně, když zdroj dokáže dodávat velký elektrický proud.
NahoruElektrická práce a výkon
Práce a výkon jsou u elektřiny chápány stejně jako u mechaniky. Jen je popisujeme pomocí elektrických veličin.
Výkon elektrického proudu
Elektrický proud protékající spotřebičem má výkon roven součinu proudu a napětí na spotřebiči. Tedy:
P=U\cdot I
Je tedy přímo úměrný jako proudu tak napětí.
Příklad: Jedna žárovka
Tužková baterie 1,5 V přímo napájí žárovku, kterou teče 0,5 A. Jaký je výkon dodávaný žárovce?
- Na žárovce je zřejmě celé napětí dodávané baterií (U=1{,}5\,\mathrm V)
- Teče jí proud 0,5 A (I=0{,}5\,\mathrm A)
- Proud žárovkou a napětí na ní dosadíme do P=U\cdot I.
- P=1{,}5\cdot 0{,}5\,\mathrm W=0{,}75\,\mathrm W
Příklad: Výkon LED diody
LED diodou při napětí 2 V teče proud 20 mA. Jaký je výkon tohoto proudu dodávaný diodě?
- U=1{,}5\,\mathrm V
- Pokud chceme výsledek ve wattech převedeme proud 20 mA na 0,02 A (I=0{,}02\,\mathrm{A}).
- Dosadíme do P=U\cdot I.
- P=2\cdot 0{,}02\,\mathrm W=0{,}04\,\mathrm W
Příklad: Výkon jedné z mnoha žároviček
Napětí zdroje 12 V se rovnoměrně rozdělilo na 6 stejných žároviček, kterými teče 0,1 A. Jaký je výkon dodávaný jedné žárovičce?
- Napětí připadající na jednu žárovičku je 12 děleno 6, tedy U=2\,\mathrm V
- Proud je (I=0{,}1\,\mathrm{A}).
- Dosadíme do P=U\cdot I.
- P=2\cdot 0{,}1\,\mathrm W=0{,}2\,\mathrm W
Výkon, který dodává zdroj spotřebiči označujeme jako příkon spotřebiče. To čemu říkáme výkon spotřebiče, je jen ta část výkonu, kterou spotřebič využije jak chceme (nepatří sem například tepelné ztráty žárovky).
Příklad: Výkon a příkon žárovky
Žárovkou pod napětím 12 V teče proud 1 A. Žárovka září výkonem 2 W. Je příkon a výkon stejný?
- Příkon žárovky je roven dodávanému výkonu tedy P=U\cdot I.
- Dosadíme: P=12\cdot 1\,\mathrm W=12\,\mathrm W
- Výkon žárovky (jako spotřebiče) je přimo zadaný – 2 W
- Výkon (záměrně přeměněná energie) je tedy mnohem menší než příkon (spotřebovaná energie). Zbytek jsou tepelné ztráty.
Elektrická práce
Je ve stejném vztahu k výkonu jako mechanická práce. Tedy při stálém výkonu platí W=P\cdot t. Pokud dosadíme za výkon ze vzorce výše dostaneme:
W=U\cdot I \cdot t
Je tedy přímo úměrná proudu, napětí a době provozu spotřebiče.
Příklad: Práce mixéru o známém výkonu
Mixér má výkon 20 W. Jakou práci vykoná za 100 s provozu?
- Použijeme vzorec W=P\cdot t.
- Výkon P je 20 W.
- Čas t je 100 s.
- Dosadíme: W=P\cdot t=20\cdot 100\,\mathrm J = 2000\,\mathrm J
- Vykonaná práce je 2000 J.
Příklad: Práce LED diody
LED dioda pod napětím 2 V dokonale přeměňuje proud 0,03 A na světlo. Jakou práci vykoná za 4 s?
- Použijeme vzorec W=U\cdot I\cdot t.
- Napětí U je 2 V, proud I je 0,03 A a čas t je 4 s.
- Dosadíme: W=U\cdot I\cdot t=2\cdot 0{,}03\cdot 4\,\mathrm J = 0{,}24\,\mathrm J
- Vykonaná práce je 0,24 J.
Protože je součin proudu a času roven přenesenému náboji Q, můžeme také psát W=U\cdot Q.
Příklad: Práce vykonaná přenesením náboje
Napětí 60 V přeneslo náboj 2 C z jednoho pólu zdroje na druhý. Jakou práci tak vykonalo?
- Použijeme vzorec W=U\cdot Q.
- Napětí U je 60 V a náboj Q je 2 C.
- Dosadíme: W=U\cdot Q=60\cdot 2\,\mathrm J = 120\,\mathrm J
- Vykonaná práce je 120 J.
Také práci můžeme dělit na skutečnou (odpovídající práci příkonu spotřebiče) a na užitečnou práci (odpovídá práci výkonu spotřebiče).
Příklad: Rozdíl skutečné a užitečné práce
Napětí 5 V přeneslo spotřebičem náboj 12 C. Přitom vykonal spotřebič mechanickou práci 50 W. O kolik byla užitečná práce menší než ta skutečná?
- Skutečnou práci konal zdroj při přenosu elektrického náboje, tedy W_\mathrm{skut}=U\cdot Q.
- Po dosazení W_\mathrm{skut}=U\cdot Q=5\cdot 12\,\mathrm J = 60\,\mathrm J
- Užitečnou práci W_\mathrm{uzit} jsme tentokrát dostali přímo zadanou, tedy 50 J.
- Rozdíl je tedy 10 J, které byly ztraceny (pravděpodobně se přeměnily na teplo).
Hlavně v energetice se používají alternativní jednotky práce. Jouly můžeme podle vzorce W=P\cdot t (watty krát sekundy) pojmenovat jako wattsekundy, zkráceně Ws.
Když tedy dosadíme watty a sekundy, dostaneme práci v joulech neboli wattsekundách. Pokud dosadíme výkon ve wattech a čas v hodinách, dostaneme výsledek ve watthodinách. A pokud dosadíme výkon v kilowattech a čas v hodinách, dostaneme známé kilowatthodiny.
NahoruElektrický proud v látkách
Víme, že elektrický proud je usměrněný pohyb nabitých částic. Jak ale elektřina proudí v různých materiálech?
- Vodiče a izolanty – Některé látky proud vedou dobře, jiné prakticky vůbec.
- Odpor vodiče – Jaký elektrický odpor má drát podle svého materiálu, délky a tloušťky.
- Teplotní závislost odporu vodiče – Co se děje s odporem drátu, žárovky nebo rezistoru, když jej zahřejeme nebo ochladíme.
- Ohmův zákon pro část obvodu – Základní vztah mezi odporem součástky (části obvodu), protékajícím proudem a napětí na ní.
- Ohmův zákon pro celý obvod a zkrat – Rozšíření Ohmova zákona na celý elektrický obvod. Vnitřní odpor zdroje napětí vysvětlí i to, proč není proud ve zkratu nekonečný.
- Polovodiče – Materiály na kterých stojí i váš mobil. Fungují právě díky tomu, že se v nich elektřina chová jinak než ve vodičích (a izolantech).
Vodiče a izolanty
V pevných látkách je elektrický proud převážně veden volnými elektrony. V kapalinách a plynech vedou elektřinu hlavně ionty. Podle toho, jak je daná látka schopna vést elektřinu, rozlišujeme vodiče a izolanty.
Vodič
Látka, kterou se snadno pohybují elektricky nabité částice a tedy dobře vede elektrický proud.
- zejména kovy, ale také materiály jako grafit (tuha)
- kapaliny s velkým množstvím rozpuštěných iontů (mořská voda je celkem dobrý vodič)
- plyny pod vysokým napětím (blesk) nebo teplotou (Slunce) –tzv. plazma.
Izolant
Pravý opak vodiče – látka, která neumožňuje pohyb nabitých částic a prakticky nevede elektrický proud.
- většina běžných nekovových materiálů jako plasty, sklo, (suché) dřevo, papír, guma
- kapaliny s minimem iontů (destilovaná voda)
- plyny za běžných podmínek
Pokud elektricky nabijeme vodič, mohou se po něm nabité částice přesouvat (například když je přivedeme všechny na jedno místo rozprostřou se, nebo když přiblížíme souhlasně nabité těleso, utečou na vzdálenější konec, ) nebo rozprostřít. Pokud ale nabijeme izolant, musí nabité částice zůstat na těch místech, kam jsme je přivedli.
NahoruVýpočet odporu vodiče
I dobré vodiče mají elektrický odpor (nulový odpor mají jen supravodiče).
Záleží na materiálu i na rozměrech vodiče. K zjištění odporu drátu potřebujeme konkrétně znát:
- typ materiálu (rezistivita \rho, s jednotkou Ω⋅m)
- průřez vodiče (S)
- délka vodiče (l)
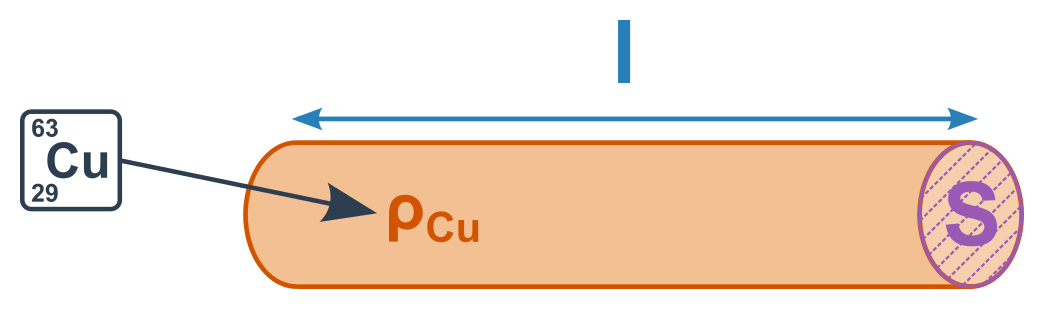
Odpor vodiče R se pomocí těchto parametrů spočítá jako:
R=\rho\frac{l}{S}
Co z toho také plyne?
- Čím delší drát, tím větší odpor (a naopak).
- Čím tlustší drát, tím menší odpor (a naopak).
Zajímavosti
- Délku vodiče si můžeme představit jako sériové spojování odporů, proto dává smysl, že je v čitateli.
- Průřez vodiče si můžeme představit jako paralelní spojování odporů, proto dává smysl, že je ve jmenovateli.
Teplotní závislost odporu vodiče
Odpor součástek ovlivňuje jejich teplota. Obvykle uváděné hodnoty platí pro určitou referenční teplotu t_0. Takový referenční odpor označujeme R_0. Pokud se teplota změní na hodnotu t, změní se odpor na R:
R=R_0(1+\alpha\Delta t)
kde \Delta t je rozdíl teplot t-t_0. Typicky je t_0 laboratorní teplota, např. 20 °C.
Veličina \alpha je teplotní koeficient odporu, má jednotku K⁻¹ (nebo °C⁻¹) a pro běžné vodiče má hodnoty v tisícinách K⁻¹.
Tento vztah je jen přibližný – hodí se pro teploty blízké t_0, Pokud se blížíme absolutní nule nebo tavení materiálu, je již nepoužitelný.
Příklad: teplota tak akorát
- Co když je t rovno t_0?
- Dosadíme do R=R_0(1+\alpha\Delta t).
- Máme R=R_0\cdot (1+\alpha\cdot 0)=R_0\cdot (1+0)=R_0
- Proto je odpor R roven (jak jsme očekávali) R_0.
Příklad: žhavý rezistor
- Rezistor o uvedeném R_0= 1000 \,\mathrm{\Omega} se proudem zahřál na 170 °C. Jak se změnil jeho odpor pokud \alpha=0{,}004\,\mathrm {K^{-1}}?
- Předpokládáme, že t_0 je 20 °C, takže \Delta t je 150 °C.
- Použijeme R=R_0(1+\alpha\Delta t).
- Máme R=1000\cdot (1+0{,}004\cdot 150)\,\Omega=1000(1+0{,}6)\,\Omega=1600\,\Omega
- Odpor vzrostl na 1600 ohmů.
Stejně se setkáme se zápisy R=R_0(1+\alpha\Delta T) při \Delta T=T-T_0. To je jen vyjádření faktu, že můžeme dosazovat termodynamické teploty (T) nebo teploty v Celsiově stupnici (t).
Příklad: chlazení
Jaká je R stoohmového rezistoru z materiálu o \alpha=0{,}001\,\mathrm {K^{-1}}, když jej ledujeme (0 °C)?
- R_0 = 100 \,\mathrm{\Omega}
- T_0=293 \,\mathrm K
- T=273 \,\mathrm K
- \Delta T je podle definice T-T_0 záporné (−20 K).
- Použijeme R=R_0(1+\alpha\Delta T).
- Máme R=100\cdot (1-0{,}001\cdot 20)\,\Omega=100(1-0{,}02)\,\Omega=98\,\Omega
Odpor klesl na 98 ohmů.
Pro rezistivitu materiálu platí obdobný vztah jako pro odpory, tedy \rho=\rho_0(1+\alpha\Delta t).
NahoruOhmův zákon pro část obvodu
Elektrický odpor R představuje, jak moc látka brání průchodu elektrického proudu. Pro část obvodu (například jednu součástku) s odporem R platí:
R=\frac{U}{I}
kde U je napětí na této součástce a I je proud, který jí protéká.
Příklad: neznámý odpor
- V šuplíku jsme našli rezistor s nečitelným údajem odporu. Jak odpor zjistíme?
- Můžeme jej zapojit do obvodu a naměřit napětí na něm U a jaký proud I jím teče. Pak použijeme R=U/I.
- Měřáky ukazují proud 500 mA a napětí 5 V.
- Než dosadíme do R=U/I převedeme proud na základní jednotku, tedy 0,5 A.
- R=5/0{,}5\,\Omega=10\,\Omega
- Zjistili jsme že rezistor měl 10 ohmů.
Pokud potřebujeme zjistit napětí nebo proud, upravíme R=\frac{U}{I} na tvar U=R\cdot I nebo I=\frac{U}{R}.
Příklad: nespálíme si rezistor?
Koupili jsme 10ohmový rezistor, kterým smí protékat max. 0,2 A. Můžeme jej připojit přímo k 3V zdroji?
- Chceme vypočítat maximální U.
- Použijeme tedy vztah U=R\cdot I
- Zadané R i I jsou v základních jednotkách, můžeme rovnou dosadit.
- U=10\cdot 0{,}2\,\mathrm V=2\,\mathrm V
- Maximálně můžeme na odpor připojit 2 volty. Neměli bychom jej tedy připojovat přímo na 3V baterii.
Příklad: dvě součástky pod stejným napětím
Na dvou součástkách je stejné napětí U. Kterou poteče větší proud?
- Proud je I=\frac{U}{R}
- Pokud je U stejné, rozhodne hodnota R.
- Protože je R ve jmenovateli, znamená vyšší R nižší proud.
- Vyšší proud tedy poteče součástkou s menším odporem.
Ohmův zákon pro celý obvod a zkrat
Obecné vztahy jako \mathrm{proud}=\frac{\mathrm{nap\check eti}}{\mathrm{odpor}} používané v Ohmův zákon pro část obvodu platí i pro celý obvod, jen mají tyto veličiny trochu jiný význam:
- místo napětí na prvku, máme elektromotorické napětí zdroje U_\mathrm e
- místo proudu prvkem, máme proud dodávaný zdrojem do obvodu I
- místo odporu prvku máme celkový odpor obvodu R+R_\mathrm i. Kde:
R = odpor vnějšího obvodu, tedy celého obvodu kromě zdroje.
R_\mathrm i = vnitřní odpor zdroje, tedy jak se zdroj sám brání dodávání proudu.
Pro ideální zdroj napětí je R_\mathrm i nula. Reálné zdroje dělíme na tvrdé (nízké R_\mathrm i, např. autobaterie) a měkké (vyšší R_\mathrm i, např AAA baterie). Ohmův zákon pro celý obvod tedy zní:
I=\frac{U_\mathrm e}{R+R_\mathrm i}
Napětí v obvodu a úbytek napětí na vnitřním odporu
Pokud I=\frac{U_\mathrm e}{R+R_\mathrm i} roznásobíme jmenovatelem, dostaneme:
R\cdot I+R_\mathrm i\cdot I=U_\mathrm e
Člen R\cdot I je vlastně napětí ve vnějším obvodu, neboli svorkové napětí zdroje (U).
Člen R_\mathrm i\cdot I je napětí ztracené na vnitřním odporu zdroje (U_\mathrm i).
Jinak zapsáno U_\mathrm e=U+U_\mathrm i.
Zkrat
Pokud póly AA baterie propojíme drátem (nulový odpor), nastává zkrat. Podle klasického Ohmova zákona by \mathrm{proud}=\frac{\mathrm{nap\check eti}}{\mathrm{odpor}} měl být nekonečný, ampérmetr ale ukáže jen asi 2 A (nezkoušet, baterie může explodovat, něco podpálit, atd.!)
To právě proto, že ve skutečnosti platí I=\frac{U_\mathrm e}{R+R_\mathrm i}. I když je tedy R nula, jmenovatel díky R_\mathrm i nulový nebude. Dostaneme tak vztah pro zkratový proud:
I_\mathrm{max}=\frac{U_\mathrm e}{R_\mathrm i}
NahoruPolovodiče
Polovodiče jsou látky s elektrickými vlastnostmi někde mezi vodiči a izolanty. Díky některým unikátním vlastnostem se staly nepostradatelnými pro prakticky veškerou moderní elektroniku.
- Principy polovodičů si můžete procvičit v základním cvičení, nebo (pro náročnější) ve cvičení na základy i proud v polovodiči
- Do většiny polovodičů se dnes přidávají příměsi, čímž se výrazně posílí některé jejich vlastnosti.
- Nejjednodušší polovodičovou součástkou v elektrickém obvodu je polovodičová dioda. Tvoří ji tzv. PN přechod dvou polovodičů s opačnými příměsemi.
Polovodiče: základy
Polovodiče jsou (nejčastěji pevné, krystalické) látky, které vedou proud, ale jen málo a, na rozdíl od vodičů, jejich elektrický odpor při zahřátí klesá. Tvoří je prvky (zejména z oblasti polokovů v periodické tabulce) i sloučeniny. Např. křemík (Si), germanium (Ge), arsenid gallia (GaAs), sulfid olovnatý (PbS) aj. Vyrábí se z nich diody, tranzistory, termistory a mnoho jiných součástek, na kterých závisí fungování téměř veškeré dnešní elektroniky (počítače).
Princip polovodiče
Když dodáme atomu polovodiče dost energie, může se od něj utrhnout záporný elektron. Navíc za sebou zanechá neobsazené (kladné) místo v atomu, tzv. díru.
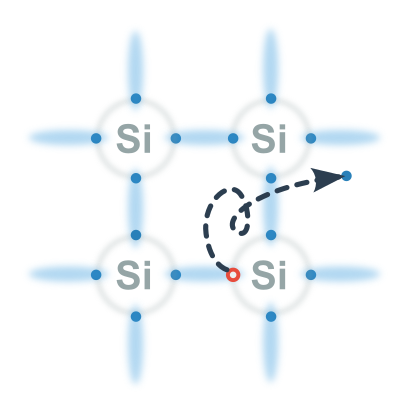
Volné elektrony a díry jsou tzv. nosiče náboje. Když totiž přiložíme napětí, budou přenášet náboj – vést proud. Každý ale jinak:
Volný elektron jednoduše letí, přitahován k +.
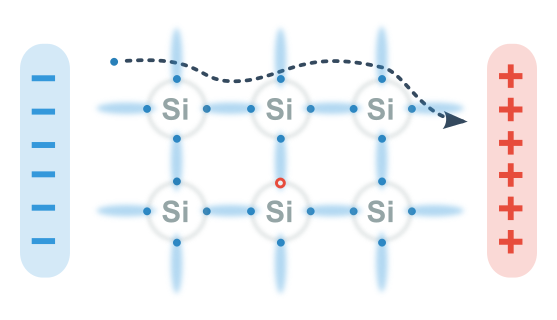
Díru se snaží zaplnit elektrony sousedních atomů přitahované k +. A tím vytvoří novou díru. Tento řetěz děr považujeme za jednu pohyblivou díru (není to tedy skutečná částice, ale jakási pseudočástice).

Pouze když díru zaplní volný elektron, oba nosiče náboje zanikají. To je tzv. rekombinace.
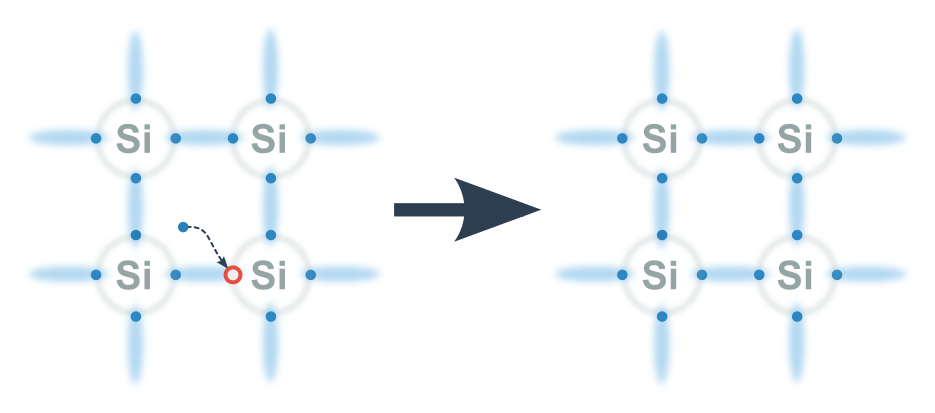
Polovodiče a proud
Polovodiče jsou (nejčastěji pevné, krystalické) látky, které vedou proud, ale jen málo a, na rozdíl od vodičů, jejich elektrický odpor při zahřátí klesá. Tvoří je prvky (zejména z oblasti polokovů v periodické tabulce) i sloučeniny. Např. křemík (Si), germanium (Ge), arsenid gallia (GaAs), sulfid olovnatý (PbS) aj. Vyrábí se z nich diody, tranzistory, termistory a mnoho jiných součástek, na kterých závisí fungování téměř veškeré dnešní elektroniky (počítače).
Princip polovodiče
Když dodáme atomu polovodiče dost energie, může se od něj utrhnout záporný elektron. Navíc za sebou zanechá neobsazené (kladné) místo v atomu, tzv. díru.

Volné elektrony a díry jsou tzv. nosiče náboje. Když totiž přiložíme napětí, budou přenášet náboj – vést proud. Každý ale jinak:
Volný elektron jednoduše letí, přitahován k +.

Díru se snaží zaplnit elektrony sousedních atomů přitahované k +. A tím vytvoří novou díru. Tento řetěz děr považujeme za jednu pohyblivou díru (není to tedy skutečná částice, ale jakási pseudočástice).

Pouze když díru zaplní volný elektron, oba nosiče náboje zanikají. To je tzv. rekombinace.

Proud v polovodiči
Celkový proud v polovodiči I je součtem proudu elektronů I_\mathrm e a proudu děr I_\mathrm d. Tedy I=I_\mathrm e+I_\mathrm d
NahoruPříměsi v polovodiči
Párů elektron-díra vytvořených tepelnou energií je v čistém polovodiči málo (např. 1 z miliardy atomů). Proto často polovodič dopujeme atomy, které mají více nebo méně valenčních elektronů.
Polovodič typu P: Pokud je elektronů méně (gallium, bór, indium, …), chová se atom, jako by měl automaticky díru.
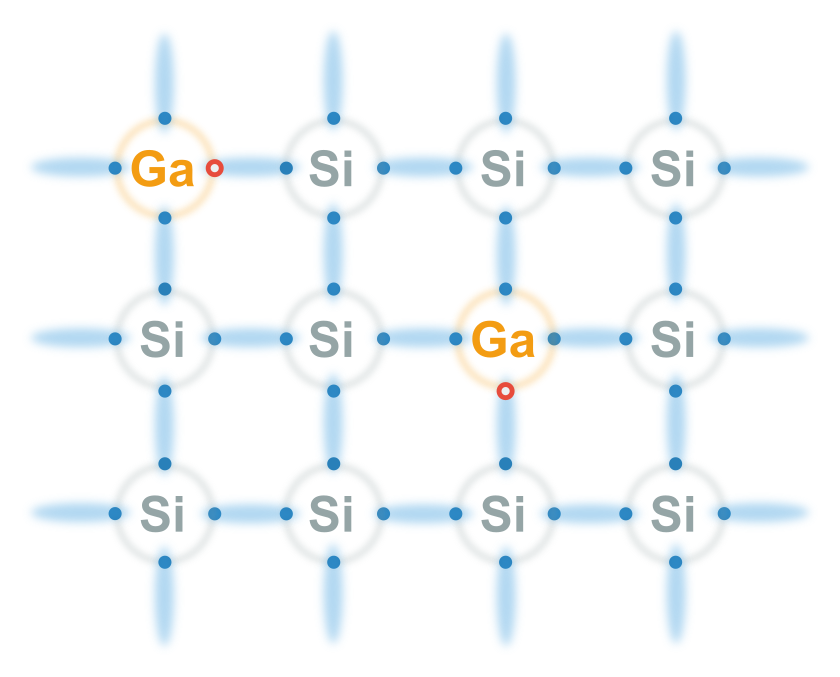
Polovodič typu N: Pokud je elektronů více (fosfor, arsen, …), elektron navíc je extrémně slabě vázán a snadno se stává volným elektronem navíc.
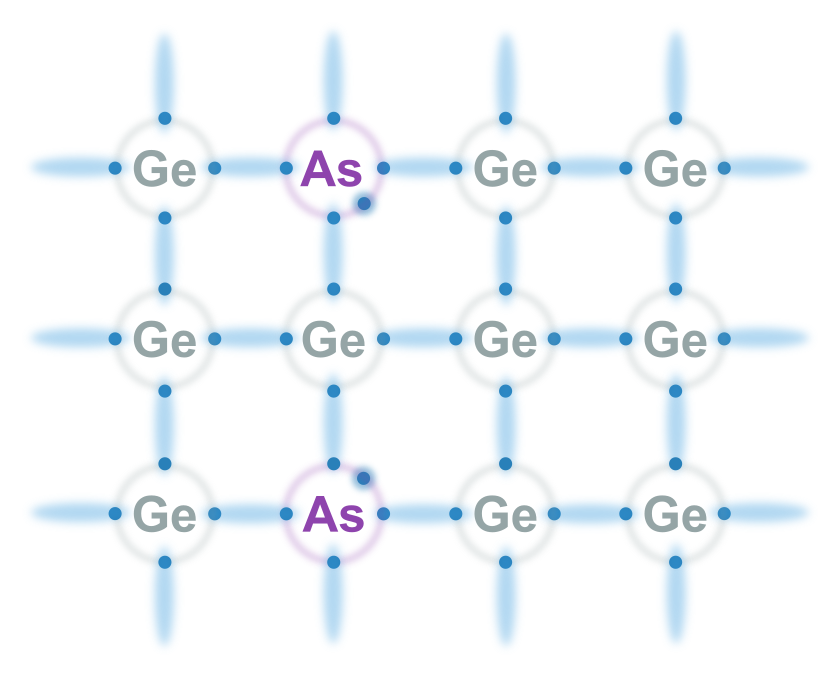
U dopovaných polovodičů není tedy stejný počet děr jako volných elektronů – máme majoritní (většinové) nosiče náboje a minoritní (menšinové) nosiče náboje.
Většinou se dopuje jen nepatrně (i když nahradíme jen každý miliontý atom, zvýšíme vodivost vzorku z 1. odstavce 1000x).
NahoruPN přechod
Už podle názvu jde o spojení dvou příměsových polovodičů – jednoho typu P (majoritními nosiči náboje jsou díry) a druhého typu N (majoritními nosiči náboje jsou volné elektrony).

Pokud je PN přechod zařazen do elektrického obvodu, získá zajímavou a důležitou funkci – propouští proud pouze jedním směrem.
- když je P připojen na + a N na − zdroje, proud prochází (propustný směr)
- když je P připojen na − a N na + zdroje, proud neprochází (závěrný směr)
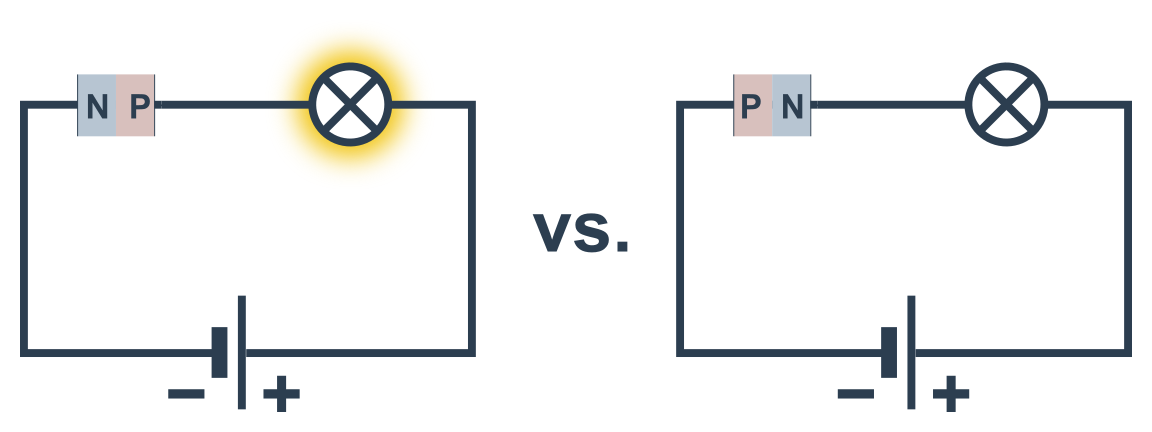
Nejjednodušší součástkou s PN přechodem je polovodičová dioda. Značíme ji šipkou a čárkou. Přitom tam, kde je čárka, je N a šipce odpovídá P strana PN přechodu.
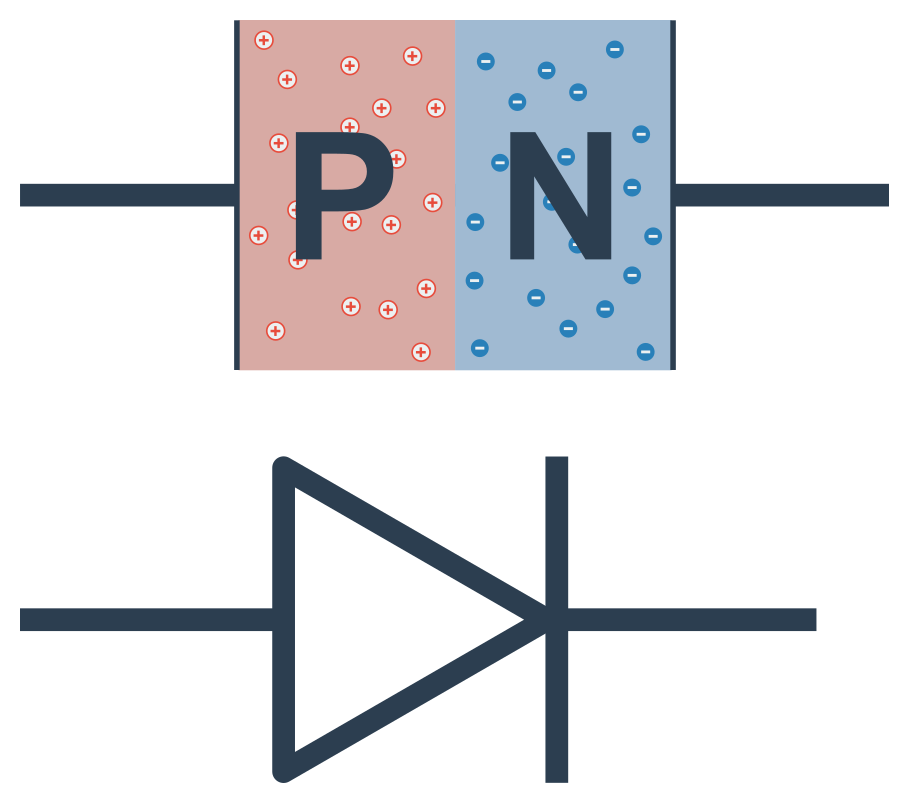
Dioda je tedy zapojena v propustném směru, když ukazuje cestu obvodem od + k −.
Přívod (konektor) diody vedoucí na P se nazývá anoda. Druhý konektor, připojený na N, je katoda.
NahoruElektrostatika
Elektrostatika studuje elektrické působení, které je statické (v čase se nemění).
Toto působení způsobují elektrické náboje, které značíme písmenem q (a případně různými indexy) a mohou být kladné (+), nebo záporné (−). Přitom dva opačné náboje se přitahují a souhlasné odpuzují, podobně jako póly magnetů.
- Coulombova síla ve vakuu – Základní kvantitativní vztah pro silové působení mezi náboji. Velmi se podobá Newtonovu gravitačnímu zákonu.
- Coulombova síla v látkách a permitivita – Elektrické síly pro náboje obklopené číkoliv jiným než vakuem se liší o tzv. permitivitu.
- Elektrické pole a intenzita – Elektrické pole představuje mapu možného působení určitého náboje na ostatní náboje v okolí.
- Elektrické síly více nábojů – Další procvičení Coulombových sil a jejich skládání.
Coulombova síla ve vakuu
Empiricky zjištěným Coulombovým zákonem popisujeme elektrickou (Coulombovu) síla F_\mathrm e, působící mezi dvěma bodovými (nebo kulově symetrickými) elektrickými náboji. Velmi se podobá Newtonovu gravitačnímu zákonu (F_\mathrm g=G\frac{m_1\cdot m_2}{r^2}), je dalekodosahová a bezdotyková, jen zde místo hmotností vystupují velikosti nábojů q_1 a q_2.
F_\mathrm e=k\frac{q_1\cdot q_2}{r^2}
I zde síly směřují do středu druhého náboje a jsou stejně velké (akce a reakce). Mohou ale také směřovat od sebe – na rozdíl od gravitační síly totiž může být elektrická síla přitažlivá (různá znaménka náboje) i odpudivá (stejná znaménka náboje).
Tzv. Coulombova konstanta k, kterou zlomek násobíme má velikost 9 \cdot 10^9 \ \mathrm{N \cdot m^{2} \cdot C^{-2}} . Ve skutečnosti je rovna \frac{1}{4\pi \varepsilon_0}, kde \varepsilon_0 je jiná konstanta, tzv. permitivita vakua.
F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2}
Takže:
- Pokles jednoho náboje (např.q_1) na polovinu znamená pokles síly na polovinu
- Pokud budou oba náboje trojnásobné, budeme sílu násobit třemi za každý z nich. Bude tedy devítinásobná.
- Pokud stejné náboje vzdálíme na dvojnásobnou vzdálenost, bude síla čtvrtinová (děleno 2 na druhou).
Tyto vzorce platí kromě vakua skoro přesně i pro vzduch a většinu plynů (málo molekul ve velkém prostoru). V jiných materiálech musíme výpočet upravit o vliv materiálu, tzv. permitivitu prostředí a počítat i s ní.
Elektrické síly mezi nabitými objekty bývají jsou mnohem silnější než ty gravitační. Např. dvě koule o náboji 1 C by se na 1 m odpuzovaly silou 9 giganewtonů. Ještě štěstí, že je celkový náboj velkých objektů ve vesmíru (planet, hvězd, …) většinou prakticky nulový (stejné množství kladného a záporného náboje). Jinak bychom nějakou gravitaci skoro neřešili.
NahoruCoulombova síla v látkách a permitivita
Permitivita \varepsilon je vlastnost prostředí určující jak silné jsou v daném prostředí elektrické síly a elektrická pole. Obvykle ji definujeme jen pro nevodivé materiály (izolanty, čili dielektrika). Má jednotku \mathrm{F/m}, tedy farad na metr. V základních jednotkách SI je to dokonce \mathrm{C^{2} \cdot N^{-1} \cdot m^{-2}}.
Ve volném prostoru (vakuu) definujeme fyzikální konstantu – permitivitu vakua \varepsilon_0. Vystupuje v základním vzorci elektrické síly ve vakuu F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2} a má hodnotu 8{,}85 \cdot 10^{-12}\,\mathrm{F/m}.
Protože je hodnota permitivity vakua takové malé a složité číslo a u jiných materiálů to je podobné, zavedl se bezrozměrný násobitel – relativní permitivita \varepsilon_\mathrm r. O permitivitě ostatních materiálů pak většinou mluvíme v \varepsilon_\mathrm r-násobcích \varepsilon_\mathrm 0.
\varepsilon=\varepsilon_0 \cdot \varepsilon_\mathrm r
- Vzduch má permitivitu podobnou vakuu, jen 1,006x větší. (\varepsilon_\mathrm r=1{,}006)
- Voda má vysokou permitivitu, 81x větší než vakuum. (\varepsilon_\mathrm r=81)
- Ethanol má také vysokou relativní permitivitu. (\varepsilon_\mathrm r=24)
- Hodně materiálů a látek (např. oleje) má relativní permitivitu kolem 2 až 3.
Všechny běžné materiály mají relativní permitivitu větší než 1. Jen plazma se chová jako prostředí s relativní permitivitou nižší než ve vakuu.
Coulombovy síly v látkách jsou rovny:
F_\mathrm e=\frac{1}{4\pi \varepsilon}\frac{q_1\cdot q_2}{r^2}
Případně pokud místo \varepsilon dosadíme \varepsilon_0 \cdot \varepsilon_\mathrm r dostaneme:
F_\mathrm e=\frac{1}{4\pi \varepsilon_0 \cdot \varepsilon_\mathrm r}\frac{q_1\cdot q_2}{r^2}
V posledním vzorci se \varepsilon_\mathrm r nachází ve jmenovateli. Takže relativní permitivita vlastně udává, kolikrát jsou elektrické síly v materiálu slabší než ve vakuu:
- Voda má \varepsilon_\mathrm r=81, takže třeba elektrická síla, která by měla ve vakuu velikost 162 N, se ve vodě zmenší na 2 N.
Elektrické síly: více nábojů
Mezi dvěma náboji (q_1 a q_2) působí elektrostatická síla F_\mathrm e=\frac{1}{4\pi \varepsilon}\frac{q_1\cdot q_2}{r^2} (ve vakuu F_\mathrm e=\frac{1}{4\pi \varepsilon_0}\frac{q_1\cdot q_2}{r^2}). Protože je r ve jmenovateli (a ve druhé mocnině), bude se vzdáleností síla F_\mathrm e klesat. Například na dvojnásobnou vzdálenost bude síla čtvrtinová.
Pokud je nábojů více, zjistíme jednotlivé síly na náboj q_1 (nebo intenzity elektrického pole E v místě, kam bychom nějaký náboj mohli umístit) od ostatních nábojů a ty pak skládáme.
Příklad: druhý náboj nulovač intuitivně
Jaký náboj na místě otazníku způsobí nulovou výslednou sílu na list papíru?
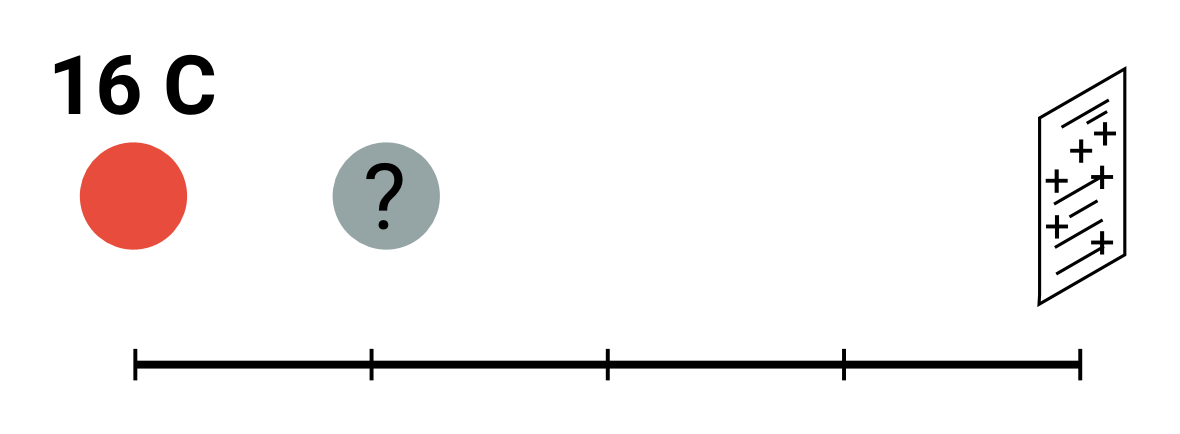
- Musí jít o záporný náboj (aby přitažlivost vyrovnávala odpuzování kladného listu a kladného náboje)
- Vzdálenosti od papíru jsou 4:3. Podle vzorce F_\mathrm e jsou účinky stejného náboje z těchto vzdáleností v poměru \frac{1}{4^2}:\frac{1}{3^2}.
- Aby byly obě působení stejná musíme tento poměr vyrovnat, různou velikostí nábojů.
- Náboje tedy budou v poměru 16:9.
Hledaný náboj je −9 C.
Příklad: druhý náboj nulovač pedantsky
Jaký náboj na místě otazníku způsobí nulovou výslednou sílu na list papíru?
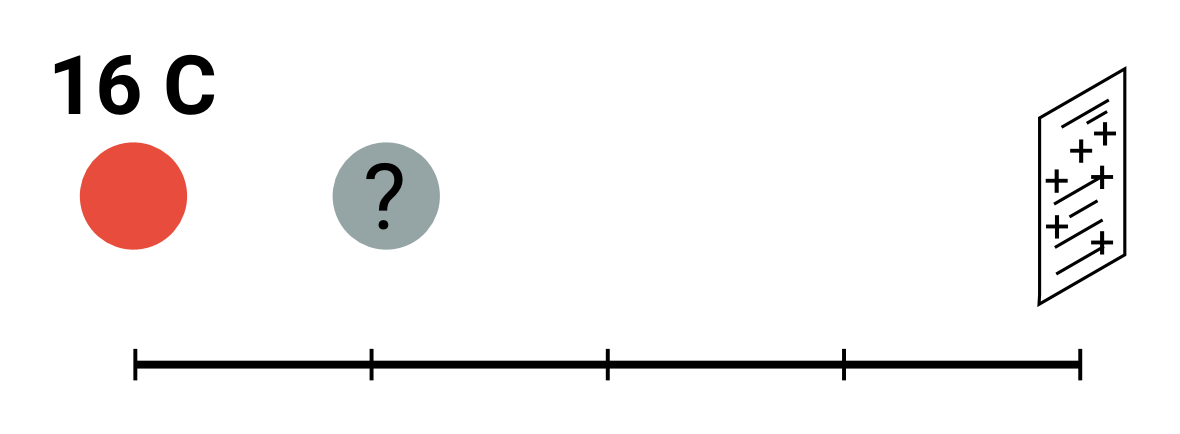
- Kladný náboj q_{+}=16\,\mathrm C odpuzuje ze vzdálenosti 4r_0 kladný papír q_\mathrm p silou F_\mathrm {e,+}.
- Aby výsledná síla vůbec mohla být nula, hledáme přitažlivou sílu. Bude tam tedy záporný náboj q_{-} ve vzdálenosti 3r_0.
- Aby výsledná síla opravdu byla nula, musí být velikost této síly F_\mathrm {e,-} stejně velká.
- F_\mathrm {e,+}=-F_\mathrm {e,-}
- Podle vzorce F_\mathrm e to je \frac{1}{4\pi \varepsilon_0}\frac{q_+\cdot q_\mathrm p}{(4r_0)^2}=-\frac{1}{4\pi \varepsilon_0}\frac{q_-\cdot q_\mathrm p}{(3r_0)^2}.
- Krátíme stejné členy: \color{red}{\frac{1}{4\pi \varepsilon_0}}\color{black}{\frac{q_+\cdot \color{red}{q_\mathrm p}}{4^2\cdot\color{red}{ r_0^2}}}=-\color{red}{\frac{1}{4\pi \varepsilon_0}}\color{black}{\frac{q_-\cdot \color{red}{q_\mathrm p}}{(3^2\cdot\color{red}{r_0^2})}}
- Zbývá tedy \frac{q_+}{16}=-\frac{q_-}{9}
- Vyjádříme hledaný q_-=-\frac{9}{16}\cdot q_{+}
q_{-}=-\frac{9}{16}\cdot 16\,\mathrm C, tedy −9 C.
Střídavý proud
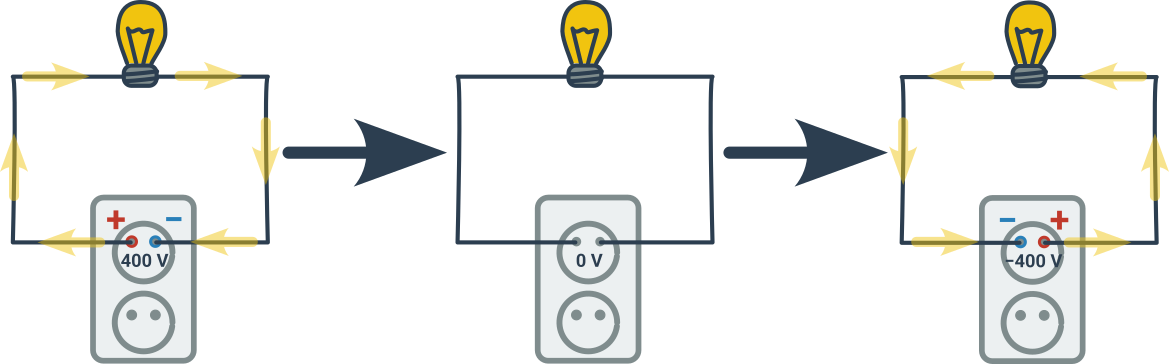
Střídavý proud je elektrický proud, který teče jednu chvíli jedním směrem a pak zase zpátky (střídá směr), protože se napětí zdroje otáčí (z pólů + a − se postupně stanou póly − a + a pak zase zpátky). Tak jak se to děje například v zásuvce:
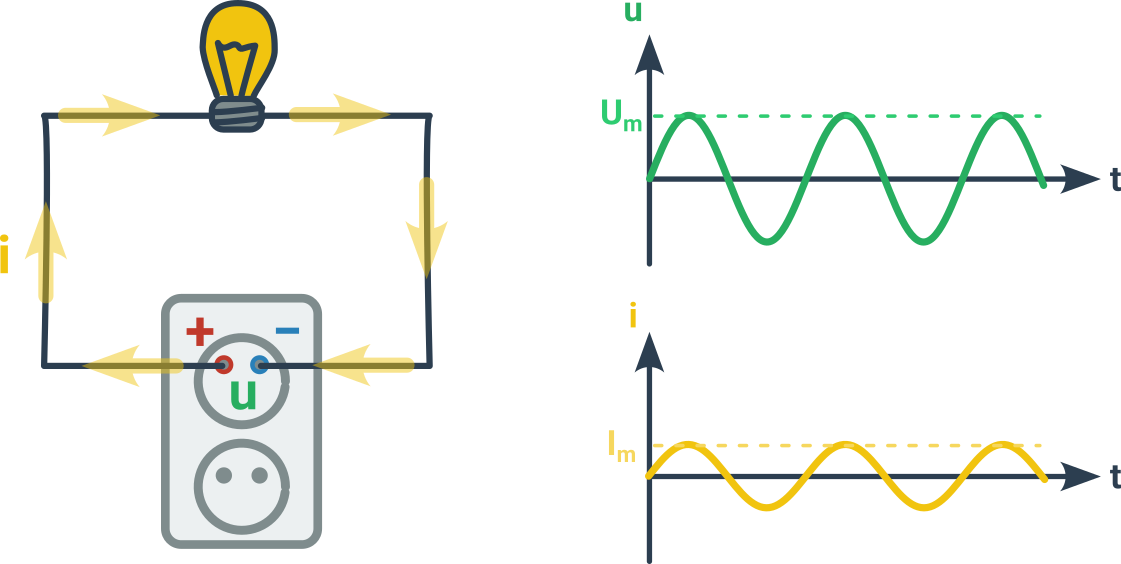
Takovéto proměnlivé napětí, které vyměňuje polaritu zdroje nazýváme střídavé napětí. V obvodu pak teče právě střídavý proud:
Obvykle pro veličiny, které se mění v čase používáme malá písmena:
u – střídavé napětí (okamžitá hodnota v určitém čase)
i – střídavý proud (okamžitá hodnota v určitém čase)
Velká písmena zůstávají pro časově nezávislé veličiny a konstanty:
U_\mathrm m – amplituda střídavého napětí (jeho maximální hodnota)
I_\mathrm m – amplituda střídavého proudu (jeho maximální hodnota)
Obvykle mají časové průběhy střídavého napětí i proudu tvar funkce sinus.
Spojování rezistorů
Rezistory jsou součástky, jejichž úkolem je klást elektřině odpor. Samy jsou někdy nepřesně označované jako „odpory“. Odbor je hlavní vlastnost rezistorů, ale mají ji i jiné součástky. Elektrická energie se v nich přeměňuje na teplo.
Hodnota el. odporu je na nich nejčastěji znázorněna textově (např. 1k2 znamená „jedno-kilo-dvě“ tedy 1200 ohmů) nebo graficky pomocí různobarevných proužků.
Často nás zajímá, jaký celkový odpor má více rezistorů v obvodu dohromady (např. pro výpočet celkového proudu obvodem). Záleží na tom, jestli jsou v obvodu spojeny sériově nebo paralelně.
Sériově zapojené rezistory
To znamená jeden za druhým (viz obrázek). Oběma mj. teče stejný proud I.
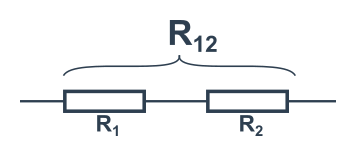
Z toho (a Ohmova zákona) se dá odvodit, že jejich celkový odpor je normálním součtem jednotlivých odporů. Tedy:
R_{12}=R_1+R_2
- Dva stejné rezistory s odporem R v sérii → celkový odpor 2R.
- Dva rezistory s odpory 100 Ω a 220 Ω v sérii → celkový odpor 320 Ω.
- Dva rezistory s odpory 2 kΩ a 2 Ω v sérii → celkový odpor 2,002 kΩ.
Paralelně zapojené rezistory
To znamená každý na jiné větvi proudu (tzv. vedle sebe, viz obrázek). Na obou musí být stejné napětí U.
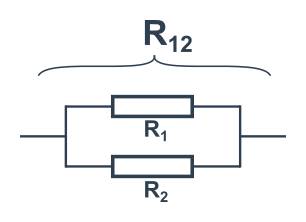
Z toho (a Ohmova zákona) se dá odvodit, že jejich celkový odpor splňuje rovnici:
\frac{1}{R_{12}}=\frac{1}{R_1}+\frac{1}{R_2}
Jde tedy o podobnou rovnici, ale s převrácenými hodnotami. Matematickými úpravami můžeme dojít k vyjádření R_{12} jako:
R_{12}=\frac{R_1R_2}{R_1+R_2}
- Dva stejné rezistory s odporem R paralelně → celkový odpor \frac{R}{2}.
- Dva rezistory s odpory 1 Ω a 4 Ω paralelně → celkový odpor \frac{1\cdot 4}{1+4}=\frac{4}{5}\,\mathrm{\Omega}.
- Dva rezistory s odpory 1 Ω a 100 Ω paralelně → celkový odpor \frac{1\cdot 100}{1+100}=\frac{100}{101}\,\mathrm{\Omega}\approx99\,\mathrm{\Omega}.
- Dva rezistory s odpory 100 Ω a 220 Ω paralelně → celkový odpor \frac{100\cdot 220}{100+220}=\frac{22 000}{320}\,\mathrm{\Omega}\approx69\,\mathrm{\Omega}.
Více rezistorů
Pro více rezistorů (a obecně více odporů) platí podobné vztahy.
Sériové zapojení N členů: R_{12..N}=R_1+R_2+R_3+\cdots+R_N
Paralelní zapojení N členů: \frac{1}{R_{12..N}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\cdots+\frac{1}{R_N}
(úprava do tvaru R_{12..N}= je samozřejmě možná, výsledné vzorce ale vypadají podle počtu rezistorů různě)
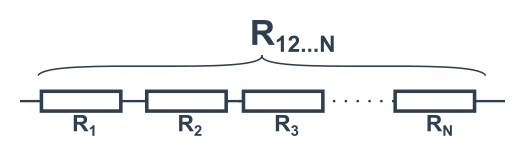
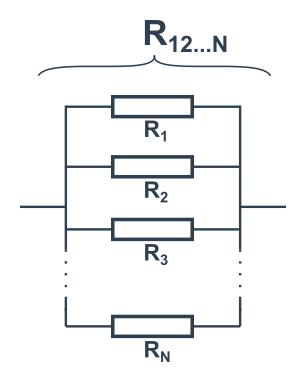
- Pět stejných rezistorů s odporem R v sérii → celkový odpor 5R.
- Tři rezistory s odpory 2 kΩ, 2 kΩ a 5 kΩ v sérii → celkový odpor 9 kΩ.
- Tři stejné rezistory s odporem R paralelně → celkový odpor \frac{R}{3}.
Složitější zapojení
Zjednodušujeme podle pravidel výše postupně od nejmenších vnitřních celků (dvojic).
Takto ano: 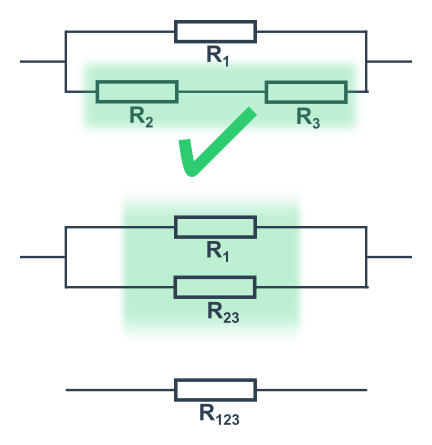
Takto ne (vybraná dvojice netvoří samostatné paralelní zapojení, k pravému uzlu se musí jít přes R_3):
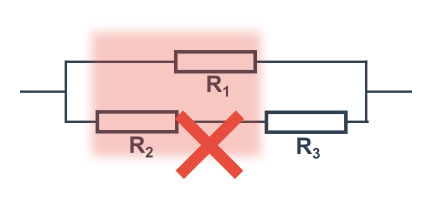
Spojování kondenzátorů
Pravidla pro počítání celkové kapacity více kondenzátorů (respektive kapacit obecně) jsou velmi podobná jako ta pro rezistory. Akorát přesně naopak.
Paralelní zapojení
Pro paralelní kondenzátory platí podobný vzorec jako pro sérii rezistorů (tedy prostý součet):
C_{12}=C_1+C_2
Případně pro více paralelně zapojených kondenzátorů je celková C rovna C=C_1+C_2+C_3+\cdots
Příklad: Dva stejné kondenzátory paralelně
Jakou kapacitu mají dva paralelně zapojené kondenzátory s kapacitou C?
- Celková kapacita je součet jednotlivých kapacit.
- C_{12} je tedy C plus C
- Odpověď je tedy 2\cdot C.
Příklad:Tři konkrétní kondenzátory paralelně
Jakou celkovou kapacitu mají paralelně zapojené kondenzátory 10 nF, 5 nF a 100 nF?
- Celková kapacita je součet jednotlivých kapacit.
- C_{123} je tedy 10 nF plus 8 nF plus 100 nF
- Odpověď je tedy 118 nF.
Sériové zapojení
Pro sériové zapojení kondenzátorů platí podobný vzorec jako pro paralelní rezistory. tedy \frac{1}{C_{12}}=\frac{1}{C_{1}}+\frac{1}{C_{2}} což můžeme upravit na
C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}
Pro více sériově zapojených kondenzátorů splňuje celková C rovnici \frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\cdots (ze které si musíme C vyjádřit).
Příklad: Dva stejné kondenzátory sériově
Jakou kapacitu mají dva sériově zapojené kondenzátory s kapacitou C?
- Použijeme C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}
- Po dosazení C_{12}=\frac{C\cdot C}{C+C}=\frac{C^2}{2C}=\frac{C}{2}.
- Odpověď je tedy \frac{C}{2}.
Příklad: Dva konkrétní kondenzátory sériově
Jakou celkovou kapacitu mají sériově zapojené kondenzátory 1 pF a 3 pF?
- Použijeme C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}
- Po dosazení C_{12}=\frac{1\cdot 3}{1+3}\,\mathrm {pF}=\frac{3}{4}\,\mathrm {pF}.
- Odpověď je tedy 3/4 pF.
Složitější zapojení
Zjednodušujeme opět od nejmenších celků, stejně jako rezistory.
NahoruVzájemné působení magnetů
Magnety na sebe mohou působit magnetickými silami. Ty (podobně jako elektrické síly) mohou být přitažlivé i odpudivé.
Magnet má vždy dva magnetické póly severní a jižní (i kdybychom magnet rozpůlili, budou oba úlomky magnety mít dva póly). Česky se póly označují jako S a J, anglicky jako N a S (north a south). Severní pól může být označen barevně (červeně).
Opačné póly se přitahují a souhlasné póly se odpuzují a to tím víc, čím blíž jsou u sebe.
K magnetům se přitahují železné věci. Používají se tedy například u modernějších kuchyňských dvířek, ve chňapkách na vaření aj. Dále je najdeme třeba v klasických HDD nebo magnetických tabulích. Přírodním magnetem je hornina magnetovec, uměle je vyrábíme například z neodymu, nebo feritů.
NahoruPůsobení magnetů na látky
Látky kolem nás můžeme dělit podle toho, jak reagují na blízkost trvalého magnetu.
- nemagnetické – vůbec na magnet nereagují
- magnetické – těleso se začne přitahovat k magnetu
Nemagnetické jsou všechny kapaliny, všechny plyny a většina pevných látek (např. guma, plast, dřevo). Magnetickými látkami se běžně myslí tzv. feromagnetické materiály. Je jich jen málo, zejména jde o některé kovy (např. železo, ocel), ale zdaleka ne všechny (třeba měď nebo hliník magnetické nejsou).
Na rozdíl od dvou magnetů se těleso z feromagnetického materiálu k magnetu vždy přitahuje. Vlastně se tedy samy stávají magnety, ale jen dočasně – dokud jsou poblíž trvalého magnetu.
Zajímavosti
Ve skutečnosti magnetické pole alespoň trošku působí na každý materiál, ale u většiny materiálů tak nepatrně, že jej zanedbáváme a považujeme je právě za nemagnetické. Tyto slabé typy působení se nazývají diamagnetismus (slabounké odpuzování, například bizmut) a paramagnetismus (slabé přitahování, například kyslík).
Elektromagnetické jevy
Často se věnujeme čistě tomu, jak funguje elektřina, elektrické pole a elektrické síly. Nebo čistě jak fungují magnety, magnetismus, magnetické pole a magnetické síly.
Tyto dva světy jsou ale propojeny:
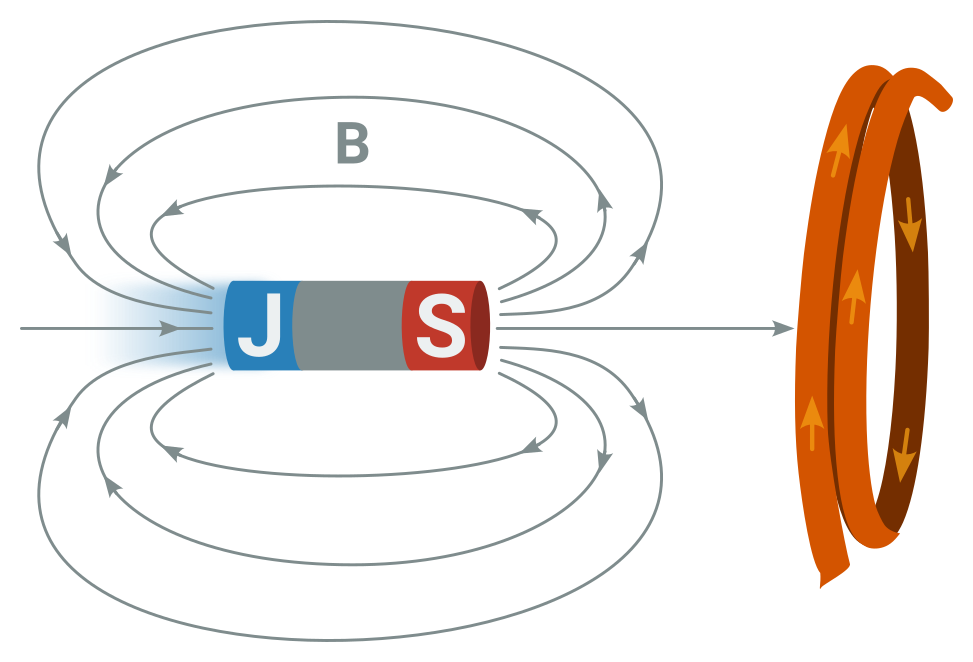
- Elektrický proud kolem sebe automaticky vytváří magnetické pole.
- Měnící se magnetické pole v blízkosti vodiče v něm umí proud vyvolat (elektromagnetická indukce).
- Většina záření kolem nás je elektromagnetického, tedy tvoří jej elektrické i magnetické pole, neoddělitelně od sebe (například rádiové vlny, mikrovlny, světlo, rentgen, \gamma-záření…).
Elektromagnetická indukce
Pokud se v místě vodiče mění magnetické pole (je tzv. nestacionární), vyvolává tato změna vznik elektrického napětí (a následně i elektrický proud).
To je podstata elektromagnetické indukce. Mnohdy je tento efekt zanedbatelný, ale zejména pro prstence nebo smyčky vodiče může být za některých okolností velmi silný a může úplně nahradit existenci zdroje elektromotorického napětí v obvodu.
NahoruElektromagnetická indukce: základy
Každá změna magnetického pole vyvolává ve vodiči vznik elektrického napětí. To je elektromagnetická indukce. Důležitá je zejména pro prstence nebo smyčky vodiče, které se tak mohou začít chovat jako zdroj elektromotorického napětí. A když je závitů vodiče víc, jako u cívky, celý efekt (velikost napětí) se násobí.
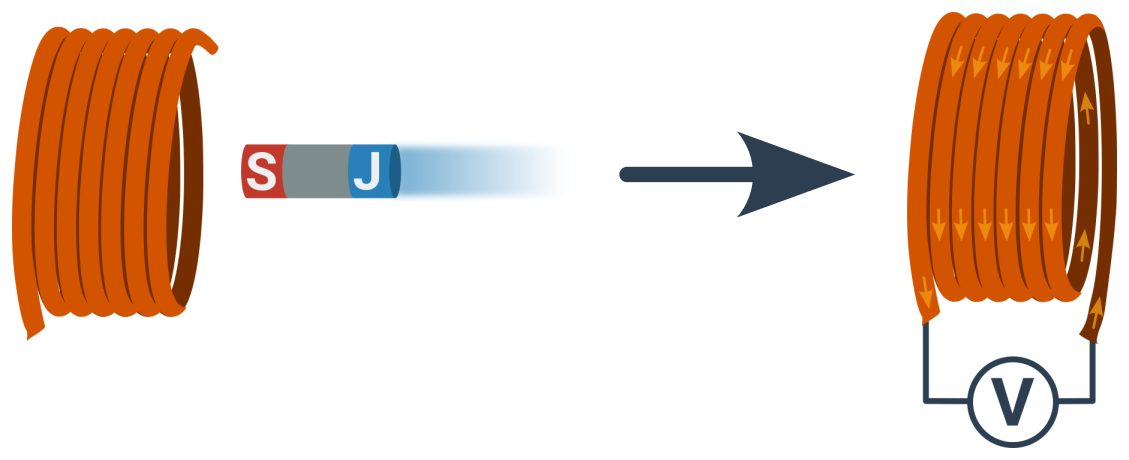
Podle Faradayova zákona vzniká ve smyčce indukované elektrické napětí U_\mathrm i úměrné rychlosti změny magnetického pole. Typickým příkladem je pohyb permanentního magnetu poblíž namotané cívky vodiče, vyvolat ji ale může i elektromagnet (druhá cívka pod proudem, viz transformátory).
Pro onen magnet a cívku je indukované napětí úměrné:
- síle magnetu (velikosti jeho magnetické indukce B)
- rychlosti pohybu magnetu
- počtu závitů cívky
Příklad: Různé cívky
- Jedna cívka má 5 závitů a druhá (stejně velká) 10 závitů.
- Druhá cívka tedy za stejných podmínek indukuje 2krát větší napětí.
Příklad: Různě rychlý pohyb
- Máme tři stejné cívky, stejně daleko od magnetu.
- K první cívce se k magnet blíží 1 m/s, ke druhé 1 cm/s a vůči třetí se nepohybuje.
- První cívka tedy indukuje 100krát větší napětí než druhá.
- Indukované napětí třetí cívky je nula.
Protože je napětí úměrné okamžité změně magnetického pole, jakmile se magnetické pole přestane měnit, indukované napětí klesne zase na nulu.
Princip elektromagnetické indukce se používá v elektrárnách ke generování střídavého napětí, i jeho transformaci na 230 V do našich zásuvek. Založeno je na ní ale mnoho dalších vynálezů – od indukčních vařičů po dynamické mikrofony.
NahoruElektromagnetická indukce: vzorce a vztahy
Elektromagnetickou indukci a indukované napětí můžeme popsat kvantitativně pomocí Faradayova zákona. Potřebujeme ale rozumět magnetickému indukčnímu toku.
Magnetický indukční tok
Vyjadřuje, kolik magnetického pole právě prochází nějakou plochou – např. průřezem smyčky vodiče. Značíme jej \Phi a jednotkou je weber.
Intuitivně si jej můžeme představit jako množství magnetických indukčních čar, které procházejí skrz smyčku (a vracejí se vnějškem). Zřejmě tedy záleží na velikosti B (obvykle jej znázorňujeme právě hustotou čar), velikostí plochy S a orientací S vůči směru B. Předpokládáme, taky že je B v rovině této smyčky alespoň přibližně homogenní. A to je vlastně celé – B, S a úhel. Přesný vzorec záleží na tom vůči, čemu tento úhel vztahujeme (jestli k rovině smyčky nebo ke kolmici na ni). Více v obrázku.
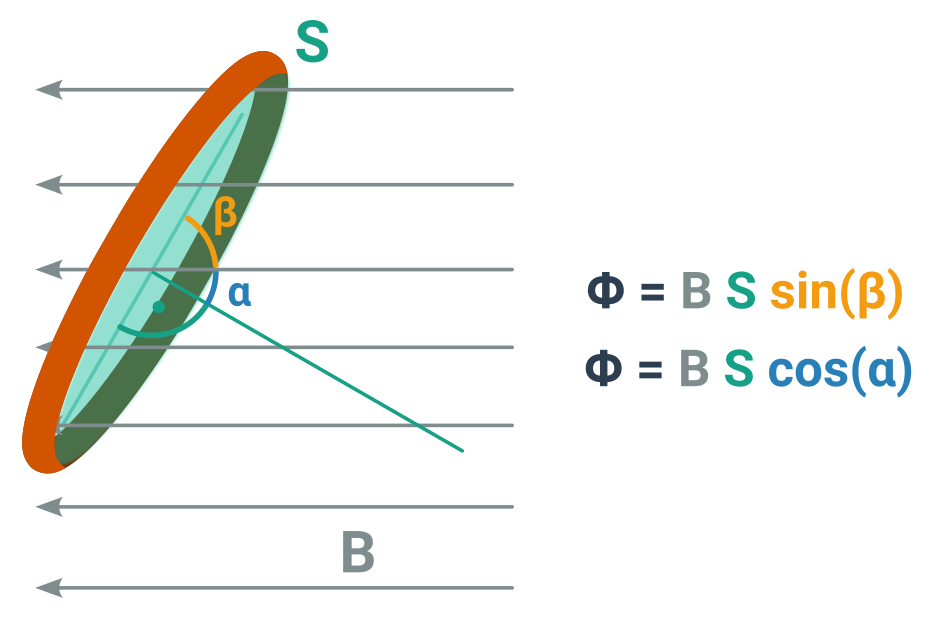
Pokud míří B kolmo na smyčku, dostaneme každopádně \cos 0° resp. \sin 90° (tedy jedničku) a tok je:
\Phi=B\cdot S
a pokud jdou rovnoběžně, dají goniometrická funkce nulu a tok je nulový.
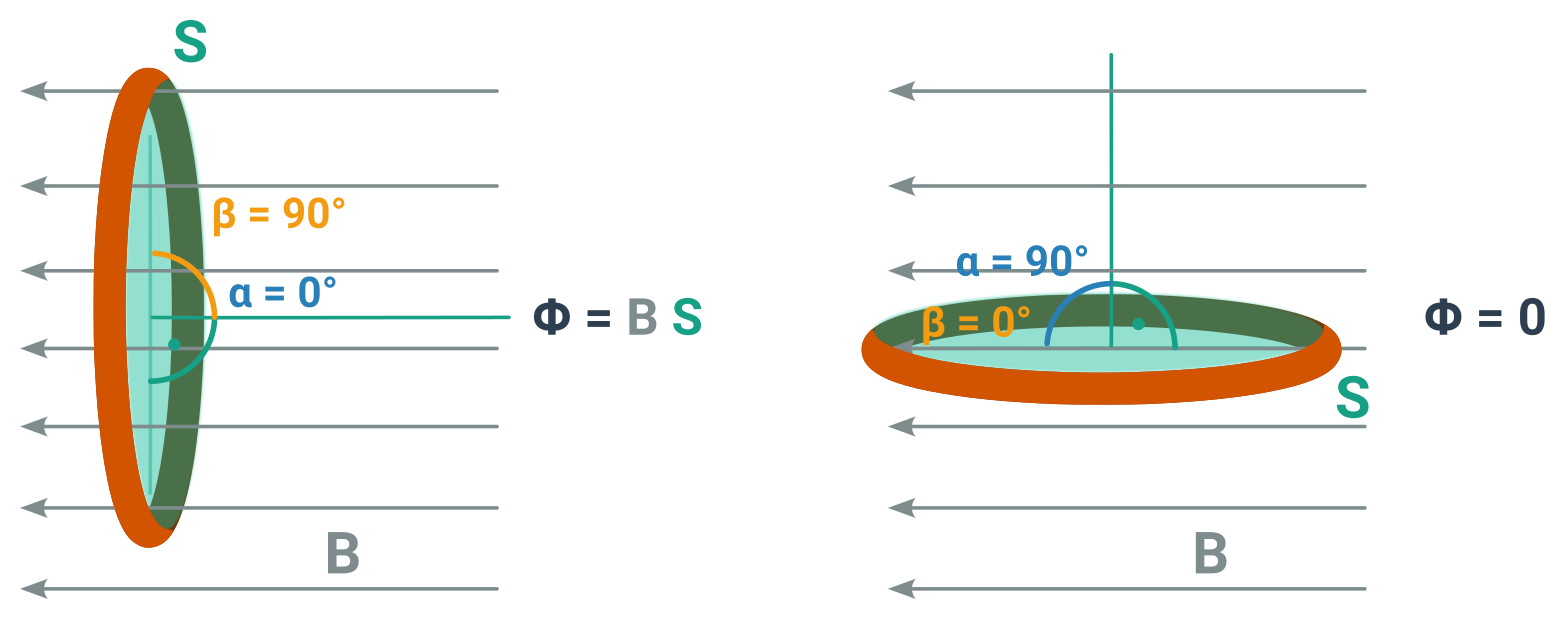
Faradayův zákon
Indukované napětí U_\mathrm i je rovno mínus změně magnetického toku za změnu času:
U_\mathrm i=-\frac{\Delta \Phi}{\Delta t}
Příklad: Přibližující se magnet
- K vodivé smyčce se přibližuje magnet:
- Smyčkou prochází čím dál tím více indukčních čar, roste magnetický tok \Phi.
- Za poslední 0,1 s (\Delta t) je rozdíl magnetického toku 0,2 Wb (\Delta\Phi).
- Dosadíme to do U_\mathrm i=-\frac{\Delta \Phi}{\Delta t}=-\frac{0{,}2}{0{,}1}\,\mathrm{V}.
- Během poslední 0,1 s bylo tedy indukované napětí (průměrně) −2 V.
Příklad: Kdy je během průletu magnetu okamžité \,U_\mathrm i \, nulové?
- K vodivé smyčce se přibližuje magnet a projde jí skrz:

- Okamžité U_\mathrm i je úměrné okamžité změně magnetického toku.
- Tok se nemění jen když je konstantní, nebo v okamžicích svého maxima nebo minima.
- Dokud se magnet přibližuje, magnetický tok \Phi roste.
- Po průchodu smyčkou se magnet vzdaluje a \Phi klesá.
- Nejvyšší magnetický tok tedy bude, když je magnet uprostřed smyčky. A právě tehdy bdue indukované napětí procházet nulou.
Příklad: Rotující prstenec v neměnném magnetickém poli
- Vodivý prstenec se otáčí v magnetickém poli. Za čas t se otočí o čtvrtinu:

- Na levém obrázku je tok \Phi roven BS.
- Na pravém obrázku je tok \Phi roven 0.
- \Delta\Phi je tedy -BS.
- \Delta t je přímo čas t ze zadání.
- Průměrné indukované napětí během tohoto pootočení je tedy U_\mathrm i=-\frac{\Delta \Phi}{\Delta t}=-\frac{-BS}{t}=\frac{BS}{t}.
Lenzův zákon
To, že pohyb magnetu vyvolává v cívce (nebo smyčce, nebo závitu, nebo prstenci vodiče) elektrické napětí a proud není vše. Co ještě se přitom děje? A kterým směrem vlastně teče indukovaný proud?
Každý elektrický proud, vytváří svoje vlastní magnetické pole, tedy i ten indukovaný. Takže pohybem magnetu vlastně vytváříme z cívky dočasně druhý magnet. A tento cívkový elektromagnet někdy reaguje přitažlivě a jindy odpudivě. Toto chování shrnul Heinrich Lenz do jednoduchého kvalitativního pravidla:
Indukovaný proud teče tím směrem, aby svým magnetickým polem působil proti změně, která jej vyvolala.
Zkusme toto abstraktní souvětí rozebrat:
- „změně která jej vyvolala“ = elektromagnetickou indukci způsobuje změna magnetického pole (pohyb permanentního magnetu)
- „působí proti změně…“ = cívka se snaží setrvat v původní vzdálenosti od permanentního magnetu, aby se tok neměnil (přitažlivě k unikajícímu magnetu a odpudivě od blížícího se magnetu). Vlastně vždy brzdí vzájemný pohyb.
- „svým magnetickým polem“ = podle přitahování/odpuzování a pólů permanentního magnetu určíme S a J pól cívky
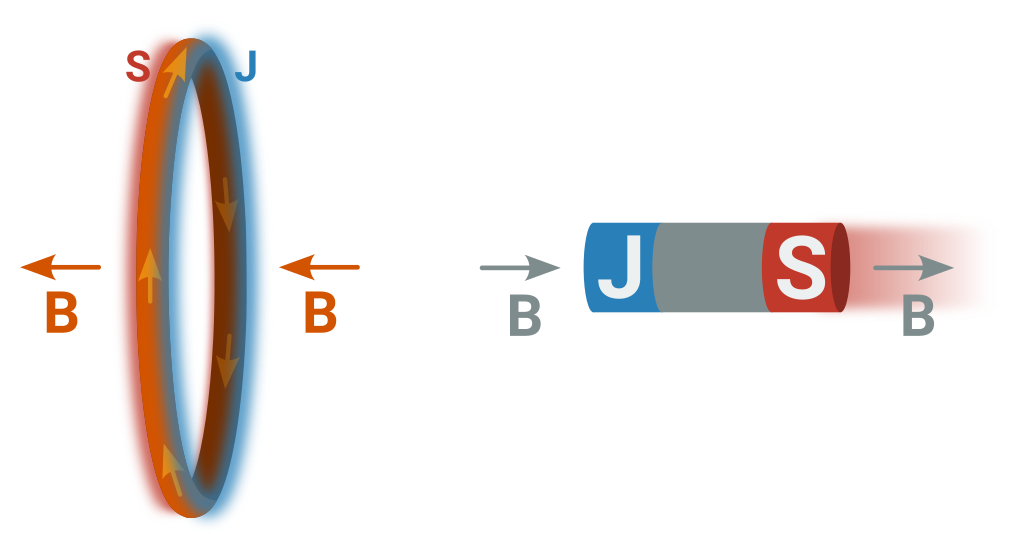
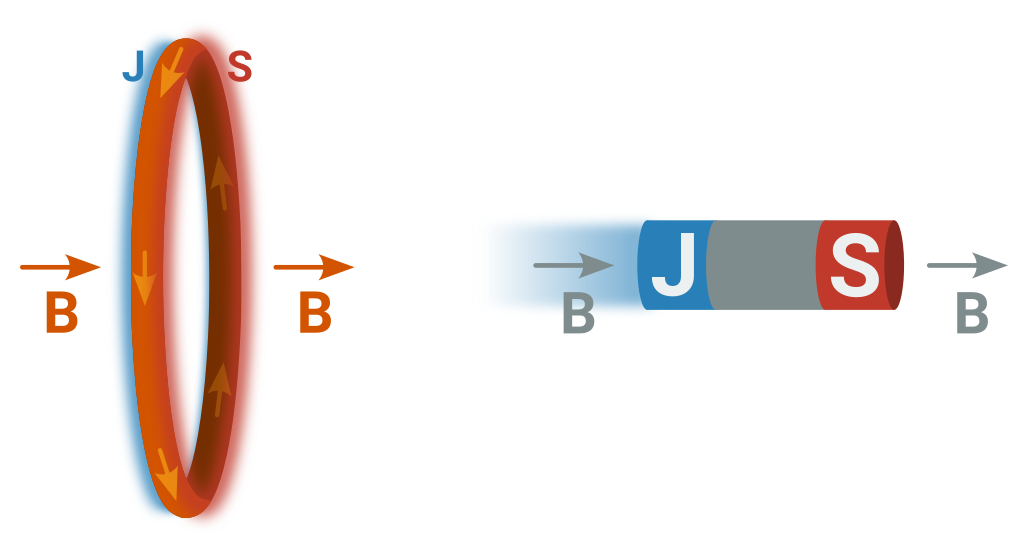
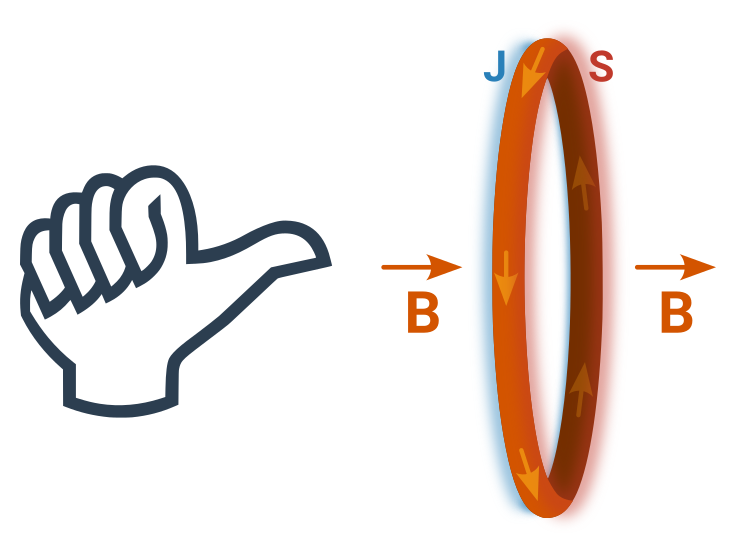
- „Indukovaný proud teče tím směrem“ = když známe S a J pól cívky, určíme (podle Ampérova pravidla pravé ruky) i směr indukovaného proudu.
Ampérovo pravidlo pravé ruky: Když dáme palec pravé ruky směrem, kterým míří severní pól/magnetická indukce, ukazují prsty směr kroužení proudu v cívce/prstenci.