Výsledek měření veličiny nemá smysl uvádět příliš přesně, pokud je samotné měření nepřesné.
Například tloušťku prkna jsme pomocí 10 měření stanovili přesně na je 17.234 mm, ale chyba měření je ± 1 mm. Může to tedy klidně být i 18 mm.
Zápis přesných tisícin milimetru je tedy nesmysl a proto výsledky měření zaokrouhlujeme (a obecně i hodnoty fyzikálních veličin). Abychom věděli jak, musíme nejprve pochopit pojem platná číslice.
Platné číslice (významné číslice)
Platné číslice jsou ty, které nesou nějakou informaci o velikosti měřené věci. První platnou číslici poznáme tak, že je to první nenulová číslice zleva.
- v čísle 350 je to 3
- v čísle 0,056 je to 5
Platné číslice jsou všechny nenulové číslice a nuly mezi nimi. Mohou to být i nuly na konci čísla pokud vyjadřují přesnost měření.
- 350 má dvě platné číslice (3 a 5)
- 0,047 má dvě platné číslice (4 a 7)
- 10,32 má čtyři platné číslice (1, 0, 3 a 2)
- 100 → může mít 1, nebo 2, nebo 3 platné číslice (záleží na tom, jak přesné bylo měření, zde to nepoznáme)
Zaokrouhlení výsledku měření
Používá se dvoukrokový postup:
- Zaokrouhlíme odchylku
Odchylku zaokrouhlíme na jednu platnou číslici, výjimečně na dvě (pokud první platná číslice je 1).
- odchylka 0,082 cm → 0,08 cm
- odchylka 1,27 cm → 1,3 cm (dvě platné číslice, protože začíná jedničkou)
- Zaokrouhlíme naměřenou hodnotu veličiny
Zaokrouhlujeme ji na stejné místo (na desítky, na tisíciny, …), na jaké jsme zaokrouhlili odchylku.
- hodnota délky je 1,0521 cm a zaokrouhlená chyba je 0,08 cm. Hodnotu zaokrouhlíme na 1,05 cm
- hodnota délky je 6,72 cm a zaokrouhlená chyba je 1,3 cm. Hodnotu zaokrouhlíme na 6,7 cm
- hodnota délky je 5 cm a zaokrouhlená chyba je 0,1 cm. Hodnotu zaokrouhlíme na 5,0 cm
Zápis
Naměřenou a správně zaokrouhlenou fyzikální veličinu pak zapisujeme ve formátu:
veličina = (hodnota ± odchylka) jednotka
Tedy například:
v=(25±3)\,\mathrm g
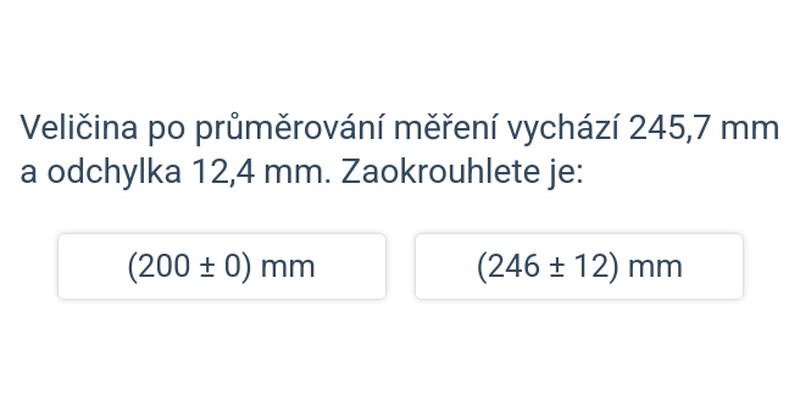
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.