Čeština
Matematika
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Biologie
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Rozhodovačka
Otázky
Slepé mapy
Pexeso
Přesouvání
Rozřazovačka
Řazení
Poznávačka
Krok po kroku
Vpisování
Porozumění
Doplňování textu
Pojmy ve větách
Označování
Situace
Poznávání zvuků
Křížovky
Roboti
Tetris
Tipovačka
Týmovka
Závody
Odkrývačka
Můj účet
Odhlásit se
Předcházející
Navazující
Cvičení
Princip páky je jedním z nejpraktičtějších využití momentu síly. Páka nám usnadňuje některé věci, na které bychom normálně neměli dostatečnou sílu, například rozlousknout ořech.
Páka a síly
Mějme těleso, které se může otáčet kolem nějaké osy nebo opěrného bodu (kleště, houpačka, zahradní kolečka). Sílu působící na jednom místě F_1 (např. tíhu nákladu) můžeme vyrovnávat druhou silou F_2 a držet páku v rovnováze. Síly působí ve vzdálenostech od osy r_1 a r_2 a nemusí být stejně velké.
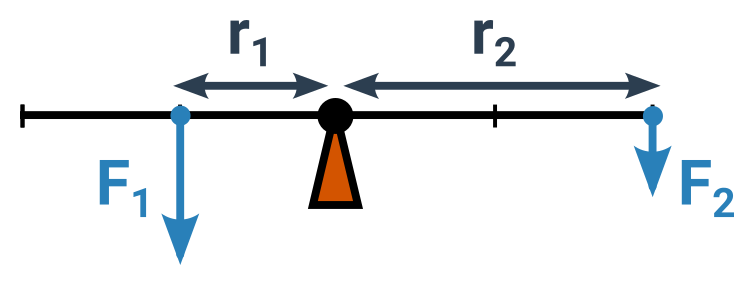
V rovnováze je poměr velikostí sil opačný než poměr jejich ramen. Zde procvičíme jednodušší případ, kdy jsou síly kolmé na úsečky r_1 a r_2. Pak je ramenem síly přímo vzdálenost od osy. Pak platí, že v rovnováze je poměr velikostí sil opačný než poměr jejich vzdáleností od osy.
F_1:F_2=r_2:r_1
Pozn.: Ve cvičeních je grafika sil pouze ilustrační – délka šipek neodpovídá velikosti sil.
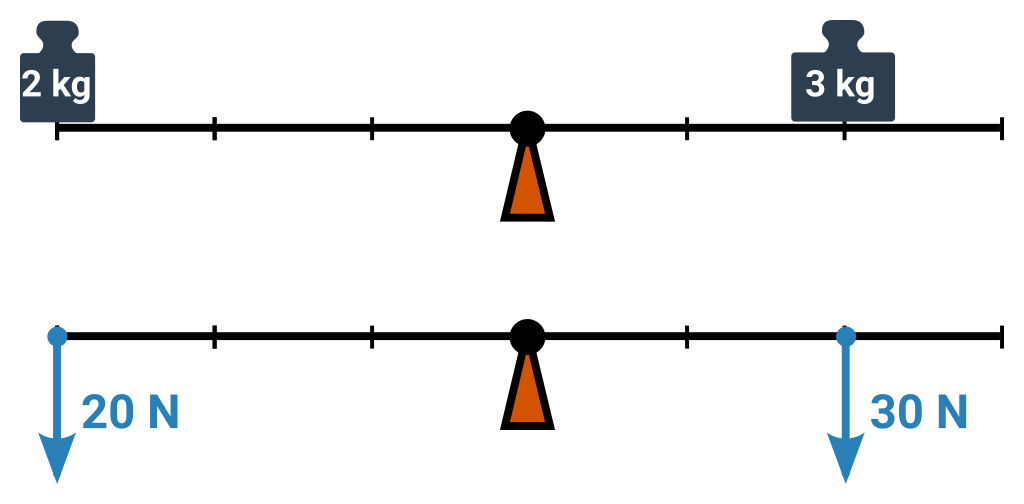
Příklad: Kdy budou síly v rovnováze stejně velké?
Síly v rovnováze nemusí být stejně velké. Ale kdy stejně velké budou?
- Platí F_1:F_2=r_2:r_1.
- Pokud jsou obě síly stejně velké, je F_1:F_2 rovno jedné.
- Jednička tedy musí být i poměr r_2:r_1.
- To znamená, že obě vzdálenosti musí být stejné.
Páka a hmotnosti
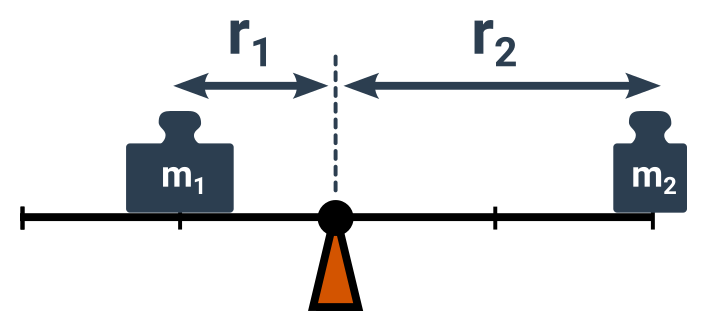
Když nepočítáme se silami, ale s hmotnostmi, platí pro rovnováhu obdobný vztah.
m_1:m_2=r_2:r_1
Příklad: Na houpačce
Kdo musí na houpačce sedět víc u středu, aby se mohli pohodlně houpat? Maminka nebo holčička?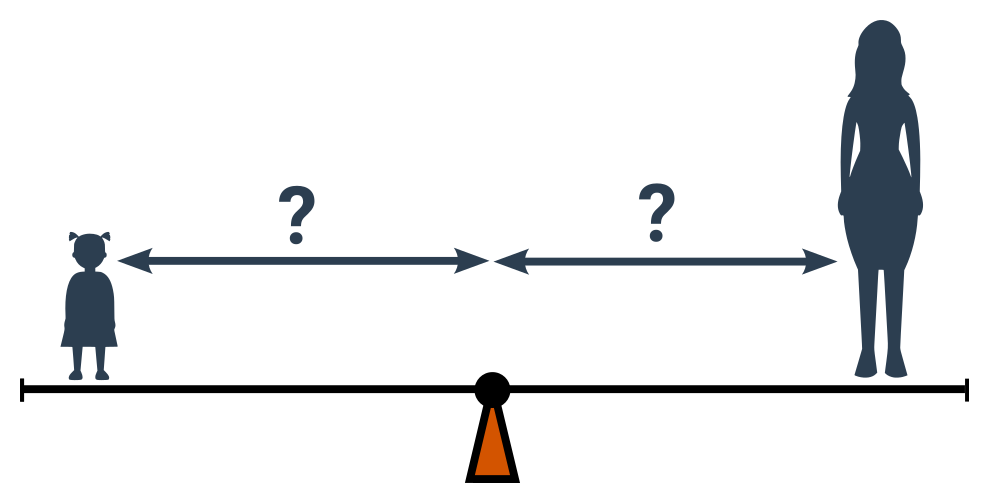 
- Rovnováha (a snadné houpání) nastane, když jsou vzdálenosti v opačném poměru než hmotnosti (m_1:m_2=r_2:r_1).
- Holčička má menší hmotnost.
- Holčička tedy musí mít větší vzdálenost od středu.
- Blíže ke středu si tedy bude muset sednou maminka.
Síly a hmotnosti dohromady
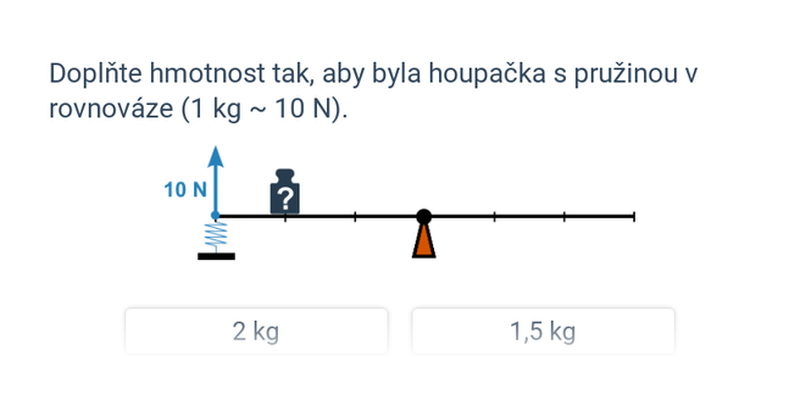
Pokud kombinujeme hmotnost a síly, musíme hmotnosti převést na tíhové síly. Každý kg odpovídá síle asi 10 N. Bedna o 3 kg, tedy bude působit silou 30 N. Člověk s 85 kg pak silou 850 N.
Příklad: Naložený trakař
Jakou silou musíme zvedat řídítka trakaře?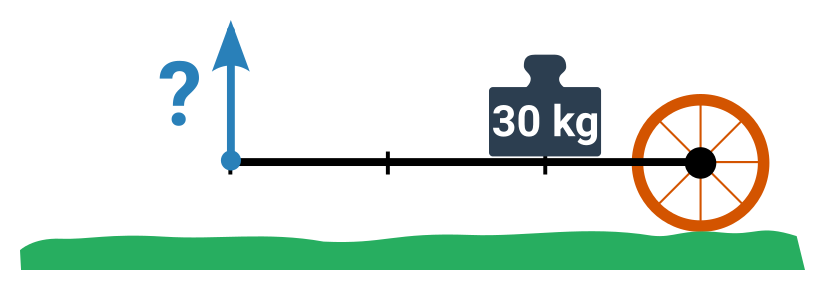 
- Kombinujeme sílu a hmotnost. Musíme tedy nejprve převést hmotnost trakaře na tíhovou sílu.
- 30 kg znamená tíhovou sílu 300 N.
- Platí F_1:F_2=r_2:r_1 – síly musí mít opačný poměr než vzdálenosti do osy.
- Poměr vzdáleností r_2:r_1 je 3 ku 1. Tedy zvedáme trakař v trojnásobné vzdálenosti od osy.
- Poměr sil tedy bude 1 ku 3. Bude tedy stačit třetinová síla (vůči těm 300 N).
- Zvedat musíme silou 100 N.
Druh páky
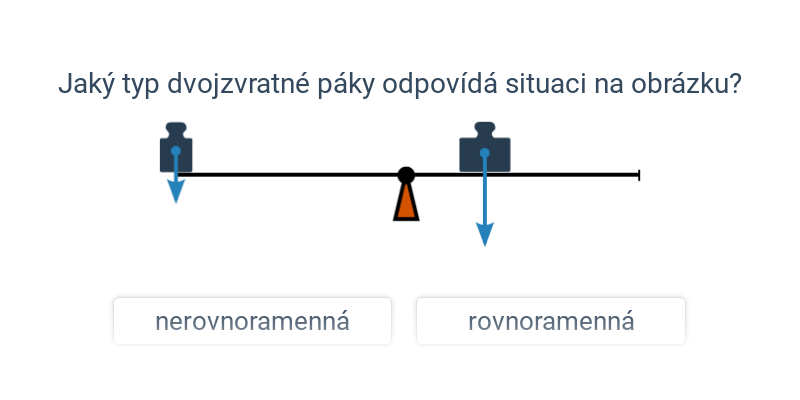
Pokud působí všechny síly na jedné straně od osy otáčení jde o jednozvratnou páku (osa otáčení je pak obvykle na kraji, např. pinzeta, trakař). Pokud působíme silami na opačných stranách od osy otáčení, jde o dvojzvratnou páku (např. kleště, nůžky, houpačka).
Proč platí podobné vztahy pro hmotnosti i síly?
- Díky přímé úměře tíhy závaží a hmotnosti (F=m g).
- Konstanta g je pro všechna závaží stejná.
- Dosadíme za F_1 a F_2 do rovnice F_1:F_2=r_2:r_1.
- Dostaneme (m_1g):(m_2g)=r_2:r_1.
- Protože m_1g:m_2g je vlastně zlomek, můžeme v něm krátit konstantu g.
- Dostaneme m_1:m_2=r_2:r_1.
