Výpis souhrnů
Termika, termodynamika, molekulová fyzika
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
První věta termodynamická
Růst vnitřní energie soustavy \Delta U je rovno součtu práce W vykonané okolními tělesy působícími na soustavu silami a tepla Q odevzdaného okolními tělesy soustavě.
\Delta U = Q + W
Pokud označíme W' jako práci vykonanou samotnou soustavou (W'= -W), můžeme jej zapsat také jako \Delta U=Q-W', neboli Q = \Delta U+W'.
Konvence +/-
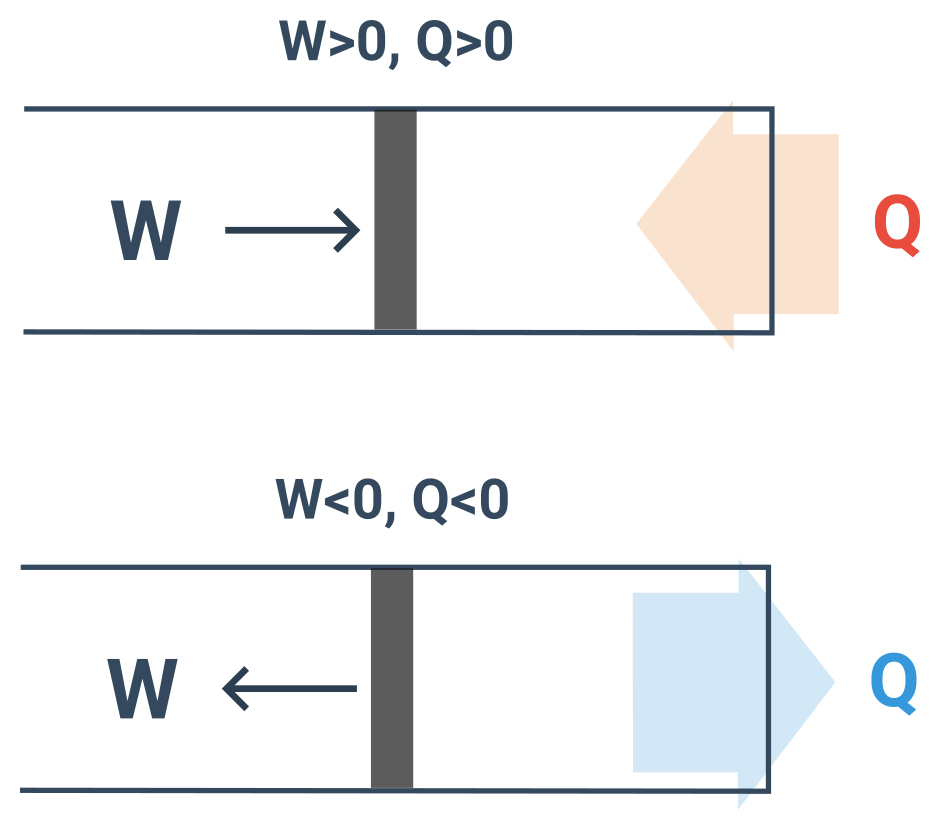
- Koná-li vnější soustava na plynu práci je W > 0, koná-li plyn práci, je W < 0.
- Přijímá-li plyn teplo je Q > 0, odevzdává-li plyn teplo je Q < 0.
Více procesů a tepelný stroj
Pokud proběhne více procesů (přijímání tepla, práce, odevzdání tepla), platí pro celkovou změnu vnitřní energie \Delta U=Q_1 +Q_1 +\cdots+W_1+W_2+ \cdots.
U stroje, který pracuje v cyklech, se U na konci cyklu vrací na původní hodnotu a \Delta U je nula.
Pak musí podle 0=Q_1 +Q_1 +\cdots+W_1+W_2+ \cdots být energie vstupující do soustavy (přijaté teplo, dodaná práce) stejná jako energie vystupující ven (odevzdané teplo, vykonaná práce).
Zajímavosti
Pokud se mění rovněž mechanická energie, potom \Delta E = \Delta U + \Delta E'
- \Delta E: změna celkové energie soustavy
- \Delta U: změna vnitřní energie soustavy
- \Delta E': změna mechanické energie soustavy
Termodynamická rovnováha a teplota
Pokud jsou dvě tělesa v tepelném kontaktu a nemění se jejich vnitřní energie, říkáme, že jsou v termodynamické rovnováze. To, co mají tato tělesa stejné, je nějaká fyzikální veličina. Nazývejme ji teplota.
Pokud si ale tělesa předávají energii, nejsou v termodynamické rovnováze a mají tedy různé teploty. Vyšší teplotu pak přiřazujeme tomu tělesu, které svou energii odevzdává druhému – mělo této vnitřní energie více. Teplota je tedy určitou mírou vnitřní energie tělesa.
Teplotu definuje mnoho různých stupnic.
Kelvinova stupnice
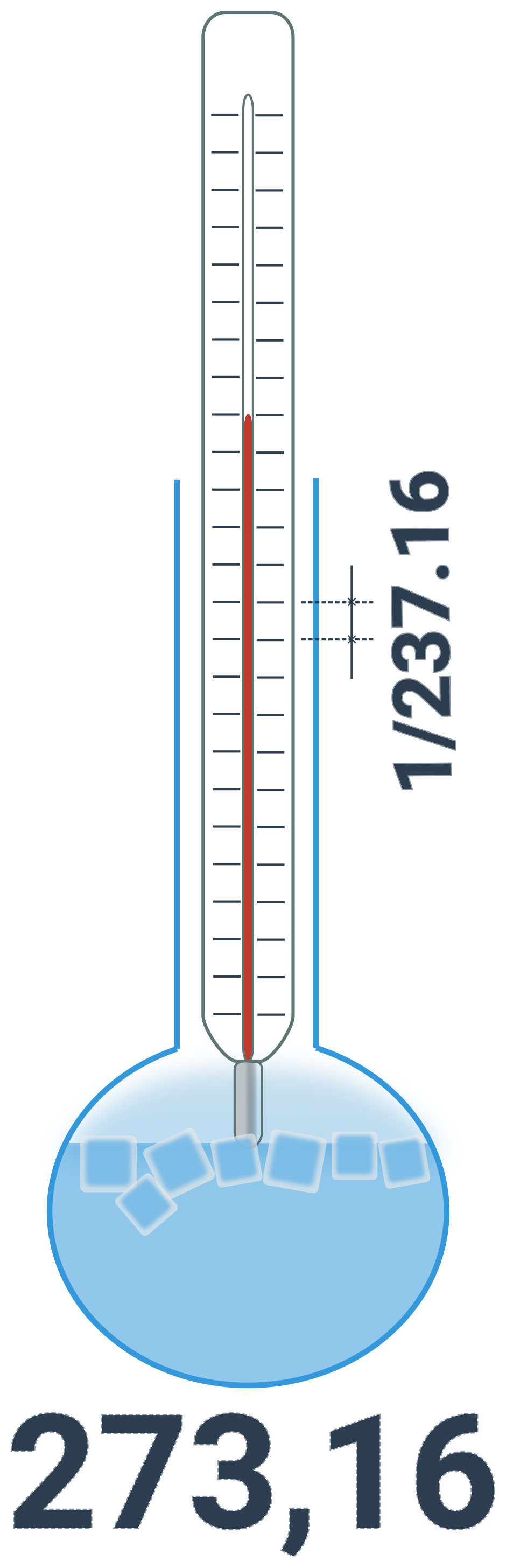
Příslušná veličina se jmenuje termodynamická teplota T. Je nejvhodnější pro fyzikální výpočty – například nemůže být záporná. Začíná totiž na absolutní nule, což je nejnižší možná teplota ve vesmíru. Její jednotka je kelvin (K), je základní jednotkou SI a definuje se pomocí trojného bodu vody:
1 kelvin = \frac{1}{273{,}16} termodynamické teploty trojného bodu vody
Celsiova stupnice
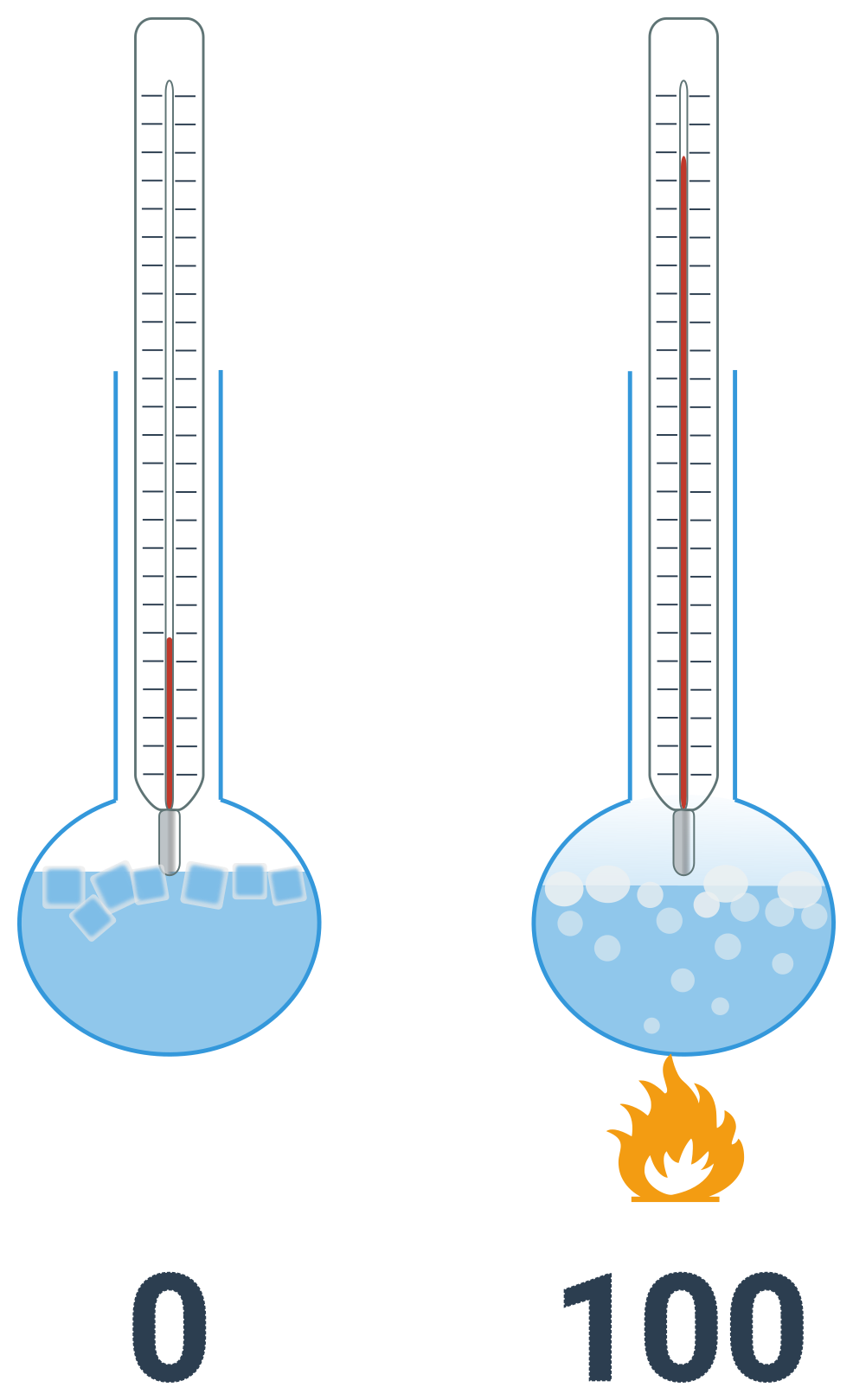
Určuje klasickou teplotu (značíme t). Je definována na základě bodů tání a varu vody za běžného tlaku. Teplotě tání je přiřazena nula a teplotě tuhnutí je přiřazeno číslo sto. Tento interval je rozdělen na sto dílů, viz obrázek níže. Jednotkou je stupeň celsia. Absolutní nula je v Celsiově stupnici rovna −273,15 °C.
Fahrenheitova stupnice
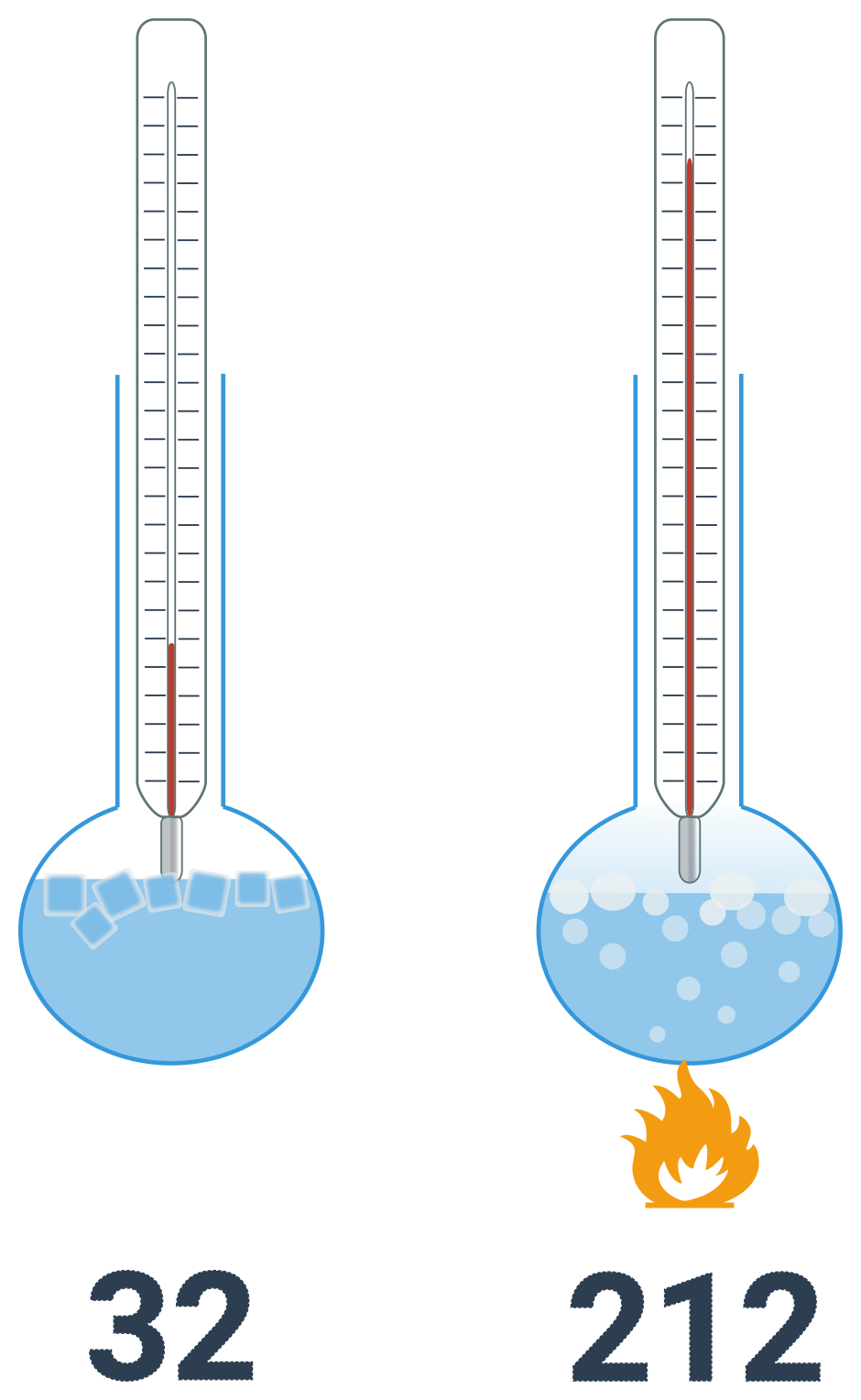
Liší se nejen posunutím, ale i velikostí jedné jednotky. Také je definována bodem tání varu vody, ale teplotě tání je přiřazena hodnota 32 a teplotě varu 212. Tento interval je rozdělen rovnoměrně na 180 dílů. Jednotkou je stupeň fahrenheita. Tato stupnice je využívána zejména v USA. Teplotu ve Fahrenheitech značíme \theta.
Převody mezi stupnicemi
Celsiova (t) a Kelvinova stupnice (T) jsou navzájem jen posunuty – o 273,15 jednotek.
Proto \{T\} = \{t\} + 273,15 a naopak \{t\} = \{T\} -273,15.
Příklad: nanuk v kelvinech
- Jakou termodynamickou teplotu má nanuk o −15 °C?**
- Dosadíme −15 °C za {t} do \{T\} = \{t\} + 273,15
- Dostaneme termodynamickou teplotu 258,15 kelvinu.
Příklad: tekutý dusík ve stupních celsia
- Jakou termodynamickou teplotu má tekutý dusík 76,5 K?**
- Dosadíme −15 °C za {t} do {t} = \{T\} - 273,15
- Dostaneme teplotu 76,5 −273,15 °C, tedy −196,65 °C.
Pro převod ze stupňů Celsia na Fahrenheity platí
\{\theta\} = \frac{9}{5}\{t\}+32 a naopak \{t\} = \frac{5}{9}\left(\{\theta\}-32\right)
Příklad: horečka ve fahrenheitech
- Jakou teplotu v \theta máme, když máme horečku 39 °C?**
- Dosadíme −15 °C za {t} do \{\theta\} = \frac{9}{5}\{t\}+32
- Dostaneme \theta = \frac{9}{5}39+32\,\mathrm{°F}=70{,}2+32 \,\mathrm{°F}=102{,}2\,\mathrm{°F}.
Zajímavosti
- Dříve se předpokládalo, že jsou při teplotě 0 K částice úplně zmraženy. Později se ukázalo, že částice kmitají v důsledku kvantové fyziky (princip neurčitosti). Tyto kmity se nazývají nulové kmity.
- Teplotních stupnic bylo vytvořeno mnohem více. Dnes se používají výhradně výše uvedené, zatímco tyto upadají do zapomnění (Rankinova teplotní stupnice (°R), Newtonova teplotní stupnice, Delislova teplotní stupnice)
Stavová rovnice ideálního plynu
Definice ideálního plynu
Jedná se o zjednodušený model skutečného plynu. Předpokládá:
- Rozměry molekul jsou zanedbatelné oproti vzájemným vzdálenostem.
- Molekuly plynu na sebe silově nepůsobí vyjma vzájemných srážek.
- Vzájemné srážky molekul a srážky molekul se stěnami nádoby jsou dokonale pružné.
Stavová rovnice ideálního plynu
Mezi veličinami popisujícími stav plynu (tlak, teplota, objem a počet částic) je spojitost – nejsou na sobě úplně nezávislé. Tento vztah můžeme vyjádřit a v případě ideálního plynu dokonce pomocí lineární závislosti:
pV = N k T
Přitom je p tlak plynu, V objem plynu, N počet částic plynu, k Boltzmannova konstanta, k = 1{,}38\times 10^{-23} \mathrm{\frac{J}{K}} a T termodynamická teplota.
Jiné tvary stavové rovnice ideálního plynu
Rovnici výše můžeme zapsat i jinak. Například pomocí látkového množství n a molární plynové konstanty R.
pV = nRT
Konstanta R je definována jako součin k s Avogadrovou konstantou N_\mathrm A. Tedy R=N_\mathrm{A}\cdot k= 8{,}31 \mathrm{\frac{J}{K\cdot mol}}.
Můžeme také použít hustotu plynu \rho a střední molekulovou (atomovou) hmotnost \mu (průměrná hmotnost částice plynu). Dostaneme tvar:
p = \frac{\rho}{\mu}kT
NahoruTepelné stroje
Tepelný stroj je cyklicky pracující soustava, která část energie dokáže přeměnit v mechanickou práci. Prvním tepelným strojem byl parní stroj, který se začal využívat v 19. století. Schematicky můžeme tepelný stroj znázornit 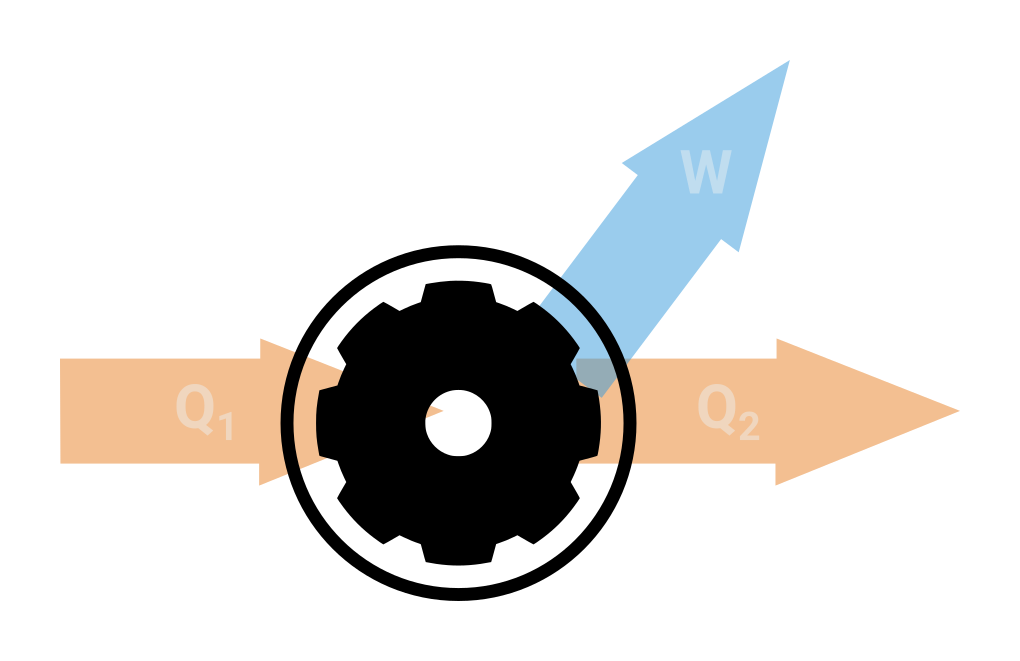
- teplo Q_1 je přiváděno z ohřívače
- teplo Q_2 je odváděno do chladiče
- vykonaná práce W
- účinnost tepelného stroje obecně spočítáme
\eta = \frac{Q_1-Q_2}{Q_1} = 1-\frac{Q_2}{Q_1} = \frac{W}{Q_1},
(může nabývat hodnot mezi 0 a 1) - vykonaná práce je dána plochou ohraničenou v pV diagramu
Co je to cyklus?
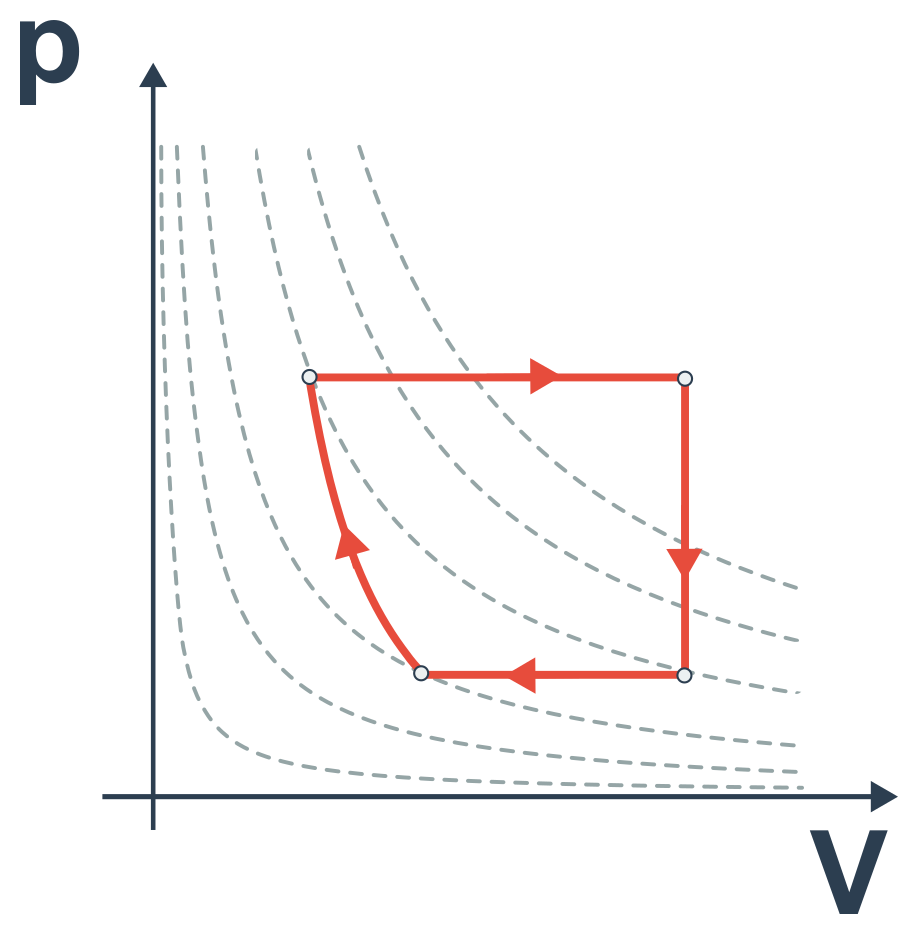
- cykly jsou po sobě jdoucí děje, které začínají a končí ve stejném bodě na pV diagramu, mohou tak probíhat opakovaně
- následující pV diagram popisuje cyklus, neboť je to uzavřená křivka:
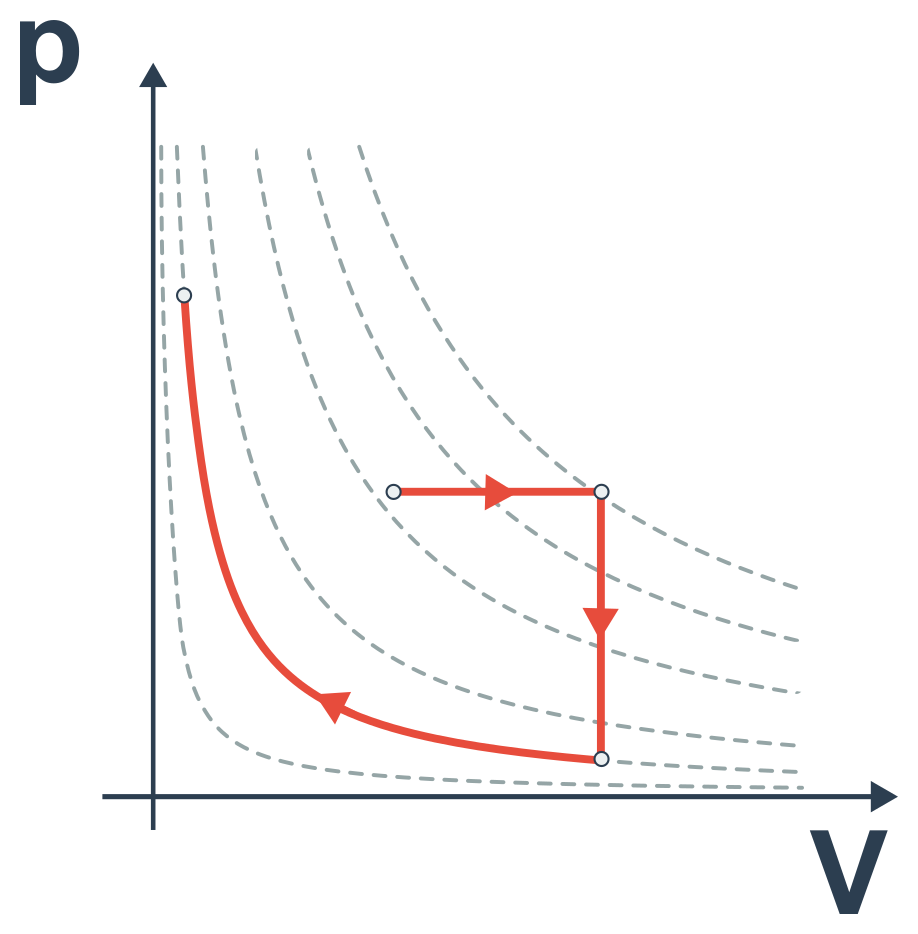
- tento pV diagram však cyklický děj nepopisuje:
Carnotův cyklus
Nejefektivnější tepelný stroj je popsán Carnotovým cyklem. Tento cyklus sestává ze čtyř dějů: 1. izotermická expanze, 2. adiabatická expanze, 3. izotermická komprese, 4. adiabatická komprese 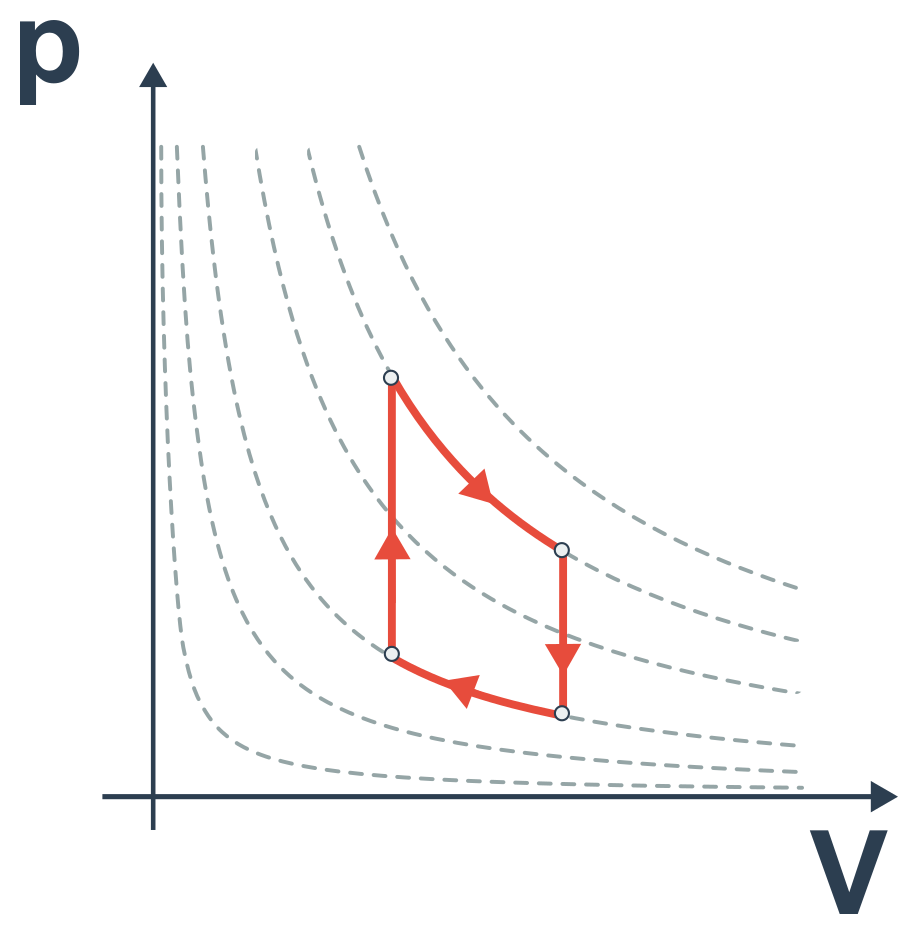 Účinnost Carnotova cyklu je rovna: \eta = 1 - \frac{T_2}{T_1}.
Účinnost Carnotova cyklu je rovna: \eta = 1 - \frac{T_2}{T_1}.
Parní stroj a spalovací motor
- nevýhodou parních strojů je jejich nízká účinnost, maximálně 15 %
- v dnešní době se využívají spalovací motory, jejich účinnost v automobilech dosahuje 35 %
Tepelná čerpadla
- v praxi se využívají i stroje, které nekonají práci, ale přečerpávají teplo
- jedním z nich je chladnička přečerpávající teplo zevnitř ven
- dalším je tepelné čerpadlo, které můžeme využívat pro ohřev místnosti i vody v bojleru
Děje v ideálních plynech
V plynech může docházet (interakcí s okolím) k procesům, kdy se mění jednotlivé stavové veličiny. To je děj v plynu.
Během děje v ideálním plynu platí stavová rovnice pV=nRT. Pro uzavřené systémy (stálé množství plynu) je konstantní R i n a máme tři proměnné stavové veličiny (p, V a T).
Často dokážeme ještě jednu z nich zafixovat (například objem pevnou velikostí nádoby). Těmto nejjednodušším dějům s pouze dvěma proměnnými stavovými veličinami říkáme izochorický děj (stálý objem), izotermický děj (stálá teplota) a izobarický děj (stálý tlak).
Významným dějem je i adiabatický děj (u něj je konstantní tzv. entropie).
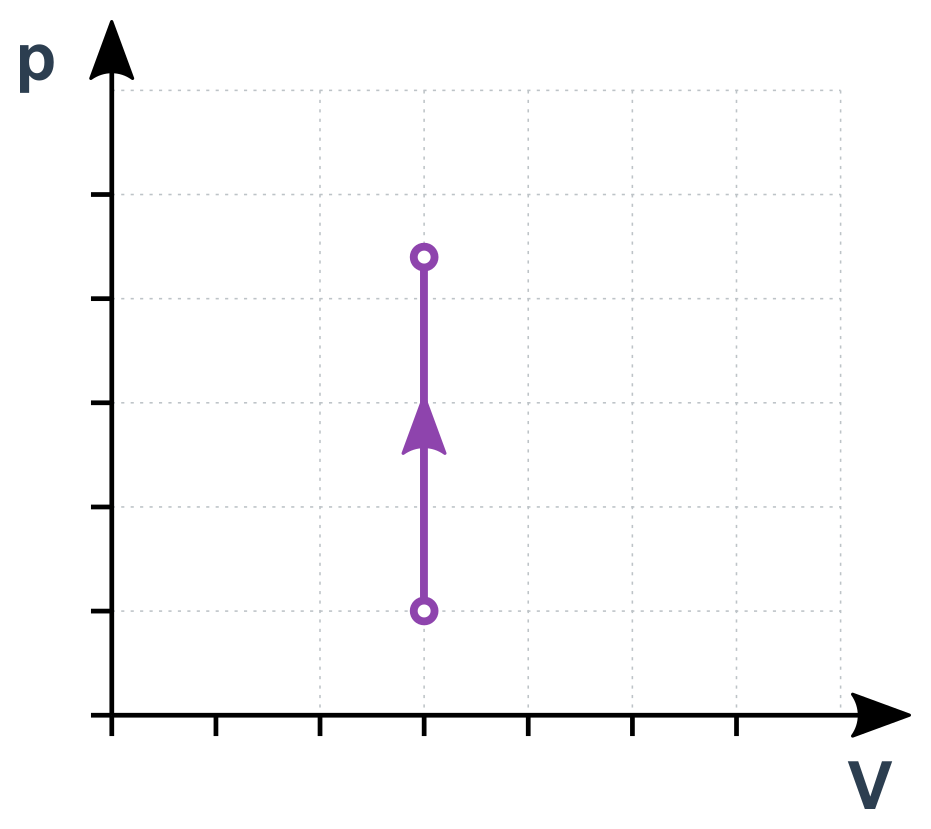
Izochorický děj (konstantní V)
Upravíme stavovou rovnici na \frac{p}{T}=\frac{nR}{V} (dělením obou stran výrazem VT). Pravá strana jsou samé konstanty, je tedy celá konstantní:
\frac{p}{T}=\mathrm{konst.}
Pro libovolné okamžiky (nebo stavy) 1 a 2 během tohoto děje tedy platí \frac{p_1}{T_1}=\frac{p_2}{T_2}. Jde vlastně o přímou úměru mezi p a T. Pokud se např. T postupně zdvojnásobuje, p současně roste také na dvojnásobek.
Izochorický děj v p-V diagramu
Izotermický děj (konstantní T)
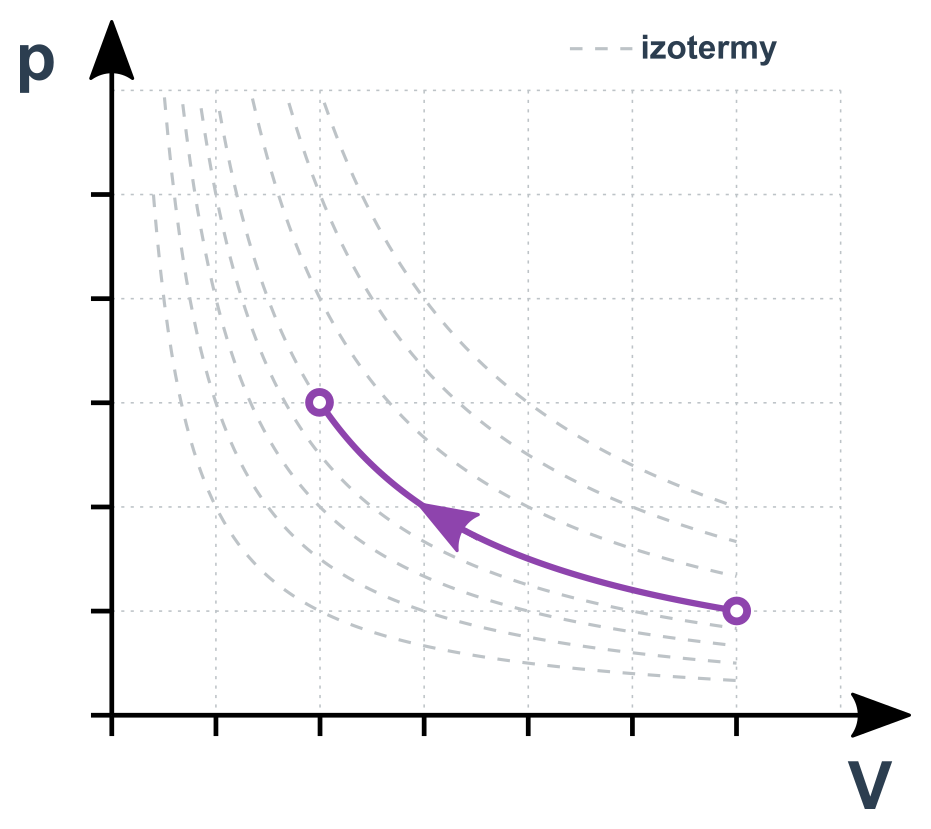
Konstantou je T, a tedy i celá pravá strana stavové rovnice:
p\cdot V=\mathrm{konst.}
Pro dva stavy 1 a 2 platí p_1\cdot V_1=p_2\cdot V_2. Jde vlastně o nepřímou úměru mezi p a V (zvětšením V na dvojnásobek klesne p na polovinu). Změny musí probíhat dostatečně pomalu, aby “topení” stíhalo udržovat plyn na stálé teplotě. Jinak by šlo o jev adiabatický (viz níže).
Izotermický děj v p-V diagramu
Izobarický děj (konstantní p)
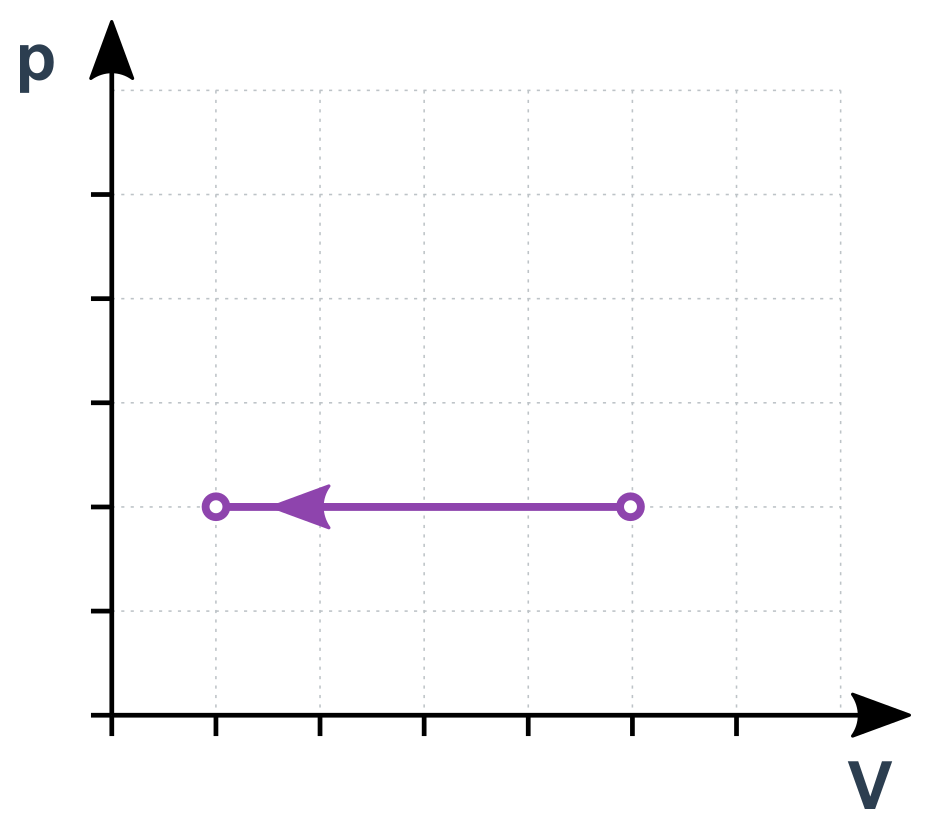
Upravíme stavovou rovnici na \frac{V}{T}=\frac{nR}{p}. Pravá strana jsou opět samé konstanty, je tedy celá konstantní:
\frac{V}{T}=\mathrm{konst.}
Pro stavy 1 a 2 můžeme psát \frac{V_1}{T_1}=\frac{V_2}{T_2}. Jde vlastně o přímou úměru V a T. Pokud se T zdvojnásobí, V bude taky dvojnásobný).
Izobarický děj v p-V diagramu
Adiabatický děj
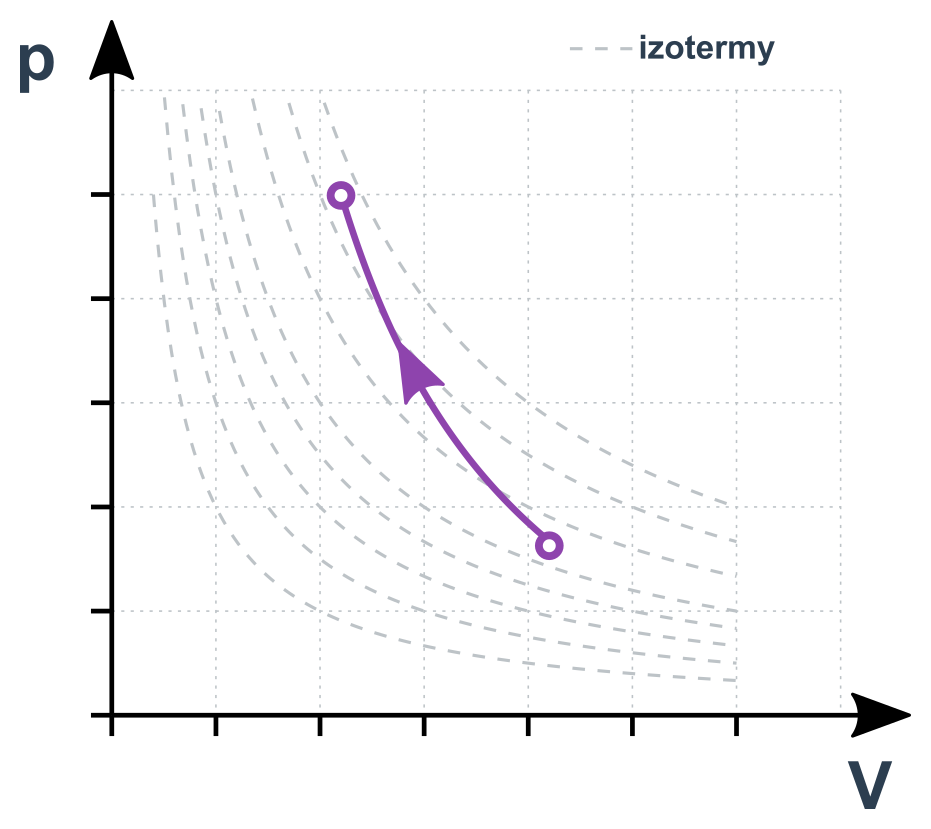
Popisuje rychlou expanzi/stlačení plynu. Vztah uvádíme přímo:
p\cdot V^\kappa =\mathrm{konst.}
Pro jednoatomové plyny je \kappa=5/3, pro dvouatomové pak \kappa=7/5. Pro stavy 1 a 2 můžeme psát p_1\cdot V_1^{\kappa}= p_2\cdot V_2^{\kappa}.
Teplota při expanzi klesá (také proto deodoranty studí) a při stlačení roste (až ke vznícení paliva ve válci diesel motoru).
Adiabatický děj v p-V diagramu
Zajímavosti
- Prakticky je nejsnáze dosažitelný děj izochorický (např. plyn uzavřený v pevné nádobě) a adiabatický (volná, rychlá nekontrolovaná expanze/stlačení).
- Pomocí p\cdot V^\kappa =\mathrm{konst.} a stavové rovnice pV=nRT můžeme vyjádřit pro adiabatický děj další vztah p\cdot T^{\frac{\kappa}{1-\kappa}}=\mathrm{konst.}
- Adiabatický děj (a pokles teploty při volném rozpínání) se používá k ochlazení zkapalňovaných plynů.
- Exponent \kappa je podíl měrného skup. tepla při stálém objemu a při stálém tlaku \kappa=c_\mathrm p/c_\mathrm V.
- Proč máme dvě verze stavové rovnice? Je to možné proto, že R byla definována jako R=k\cdot N_A a n = N/N_A (s Avogadrovou konstantou N_A). Po dosazení těchto výrazů za R a n do původní stavové rovnice p V = nRT získáme právě p V = NkT.
Vnitřní energie tělesa
Vnitřní energie tělesa U je součet celkové vnitřní kinetické energie neuspořádaně se pohybujících částic tělesa (atomů, molekul, iontů) a celkové vnitřní potenciální energie vyplývající ze vzájemné polohy těchto částic.
Součástí vnitřní energie jsou i energie jednotlivých chemických vazeb v molekulách i jaderná energie mezi protony a neutrony.
Vnitřní energii tělesa lze změnit – konáním práce, tepelnou výměnou, nebo obojím dohromady.
Změna vnitřní energie konáním práce
Působí-li vnější síla na píst válce s plynem, dochází ke stlačování plynu. Síla koná práci, která se mění právě na vnitřní energii plynu (neuvažujeme tření pístu o stěny válce).
Může to ale fungovat i naopak. To když plyn koná práci (např. vytlačuje píst) spotřebováváním své vnitřní energie.
Změna vnitřní energie tepelnou výměnou
Vnitřní energii lze měnit i prostřednictvím tepelné výměny mezi dvěma tělesy.
NahoruDruhá věta termodynamická
Není možné sestrojit periodicky pracující tepelný stroj, který by jen přijímal teplo od určitého tělesa (ohřívače) a vykonával stejně velkou práci.
Vratné a nevratné děje
Je-li děj vratný, nedochází ke změně mechanické energie na tepelnou. Z finálního stavu lze přejít zpět do počátečního stavu. Naopak u nevratných dějů to možné není. Jsou to takové, při kterých:
- se mechanická energie přeměňuje na teplo (v důsledku tření, valivého odporu, apod.)
- dochází k nevratným chemickým reakcím (denaturizace bílkovin při smažení vajec)
- mění se struktura/konzistence látky (psaní tužkou na papír)
I intuitivně a z vlastní zkušenosti víme, které děje mohou běžet pozpátku a které ne. V případě termodynamiky jsou vratnými ději adiabatický a izotermický, nevratnými ději jsou izochorický a izobarický.
Entropie
Jedna z méně intuitivních fyzikálních veličin. Lze si ji představit jako neuspořádanost systému, jinými slovy: čím je větší nepořádek, tím je větší entropie.
Celková entropie systému v čase je neklesající (nikdy se nezmenší, pouze roste, nebo maximálně zůstává stejná). Jedná se o jedno z vyjádření druhého termodynamického zákona.
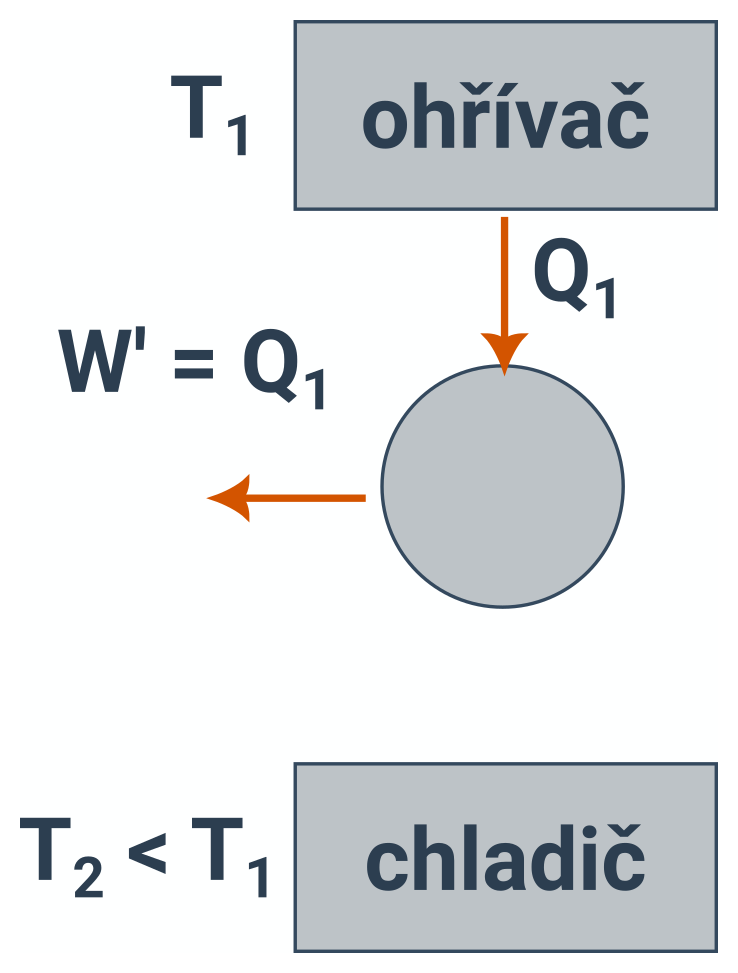 Schéma perpetua mobile.
Schéma perpetua mobile.
Entropie se při vratném ději nemění, při nevratném ději se celková entropie systému zvyšuje.
Celková energie a tepelné stroje
Energie se musí zachovávat, a tak v diagramech tepelných strojů nemůže dojít k mizení energie. To lze vidět i na následujícím schématu: 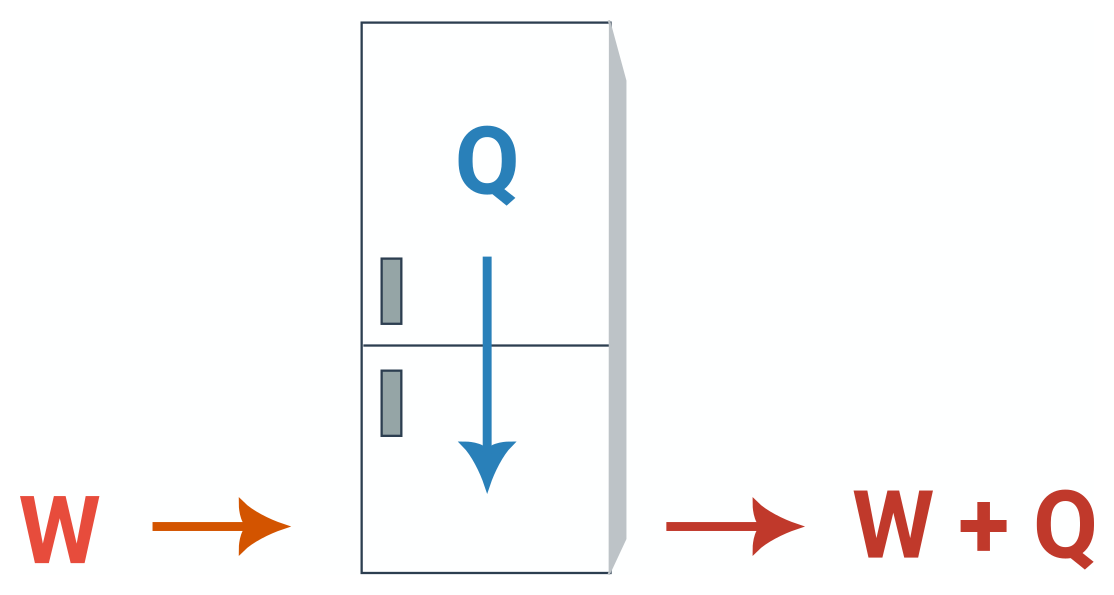 Práce vykonaná kompresorem lednice ani teplo odebrané z vnitřního prostoru nemohou nikam zmizet, a tak lednice předá do okolí teplo W + Q. Stejně to platí také pro ostatní tepelné stroje.
Práce vykonaná kompresorem lednice ani teplo odebrané z vnitřního prostoru nemohou nikam zmizet, a tak lednice předá do okolí teplo W + Q. Stejně to platí také pro ostatní tepelné stroje.

