Čeština
Matematika
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Biologie
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Rozhodovačka
Otázky
Slepé mapy
Pexeso
Přesouvání
Rozřazovačka
Řazení
Poznávačka
Krok po kroku
Vpisování
Porozumění
Doplňování textu
Pojmy ve větách
Označování
Situace
Poznávání zvuků
Křížovky
Roboti
Tetris
Tipovačka
Týmovka
Závody
Odkrývačka
Můj účet
Odhlásit seVýpis souhrnů
Rychlost, dráha, čas
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Rychlost, dráha, čas
Vztah mezi rovnoměrnou (nebo alespoň průměrnou) rychlostí v drahou s a časem pohybu t popisují vzorce:
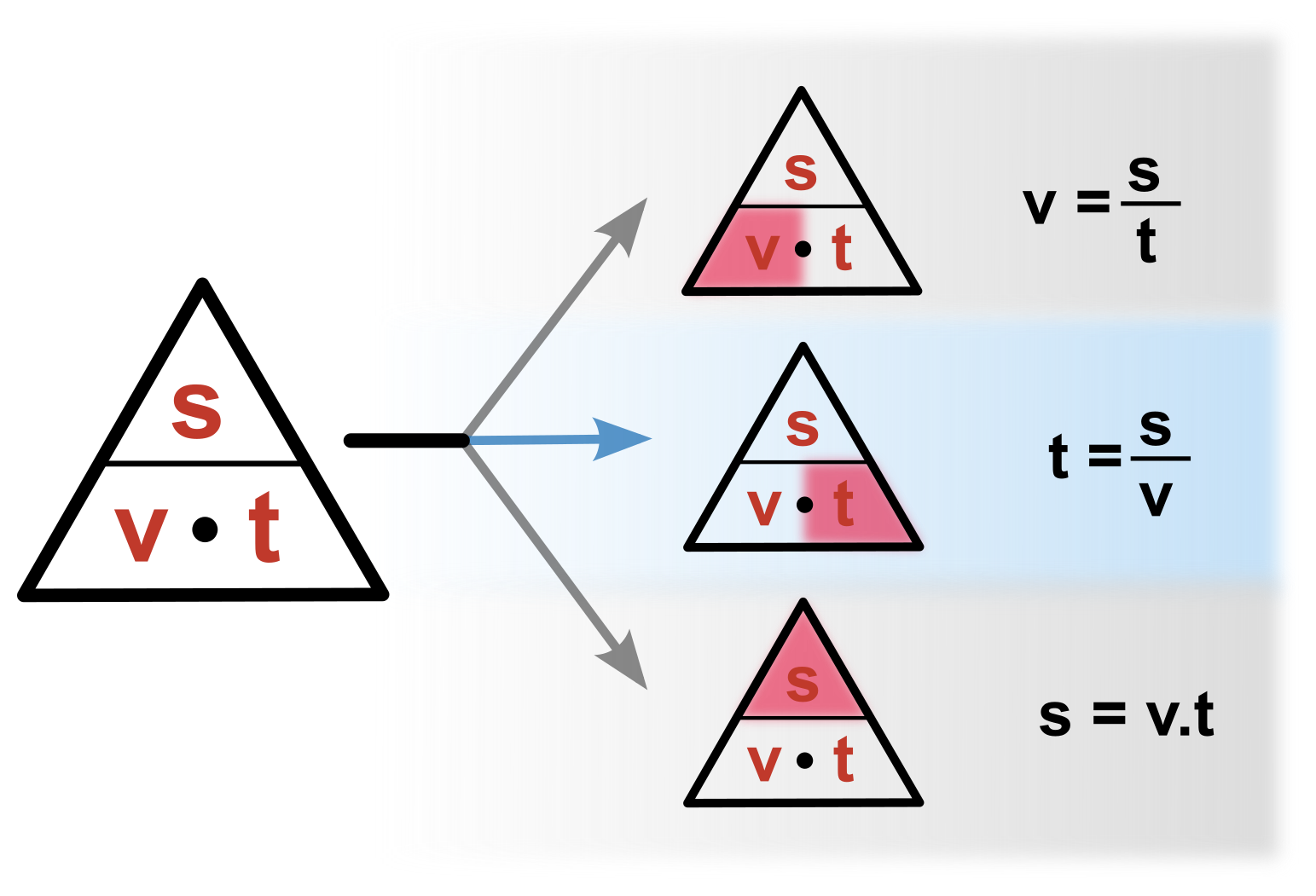
v=\frac{s}{t}
s=v\cdot t
t=\frac{s}{v}
V jednoduchých případech pouze určíme správný vzorec a dosadíme.
U mnoha pohybů těles ovšem před dosazením musíme udělat něco navíc, např. převést správně jednotky nebo určit s ze změny poloh.
Konečně můžeme pomocí těchto vztahů také řešit vzájemný pohyb více těles.
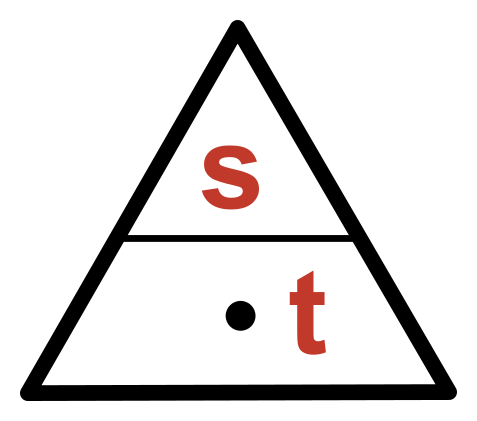
Vztahový trojúhelník (pyramida)
Pokud známe nějaký vzorec typu \bf{A=B\cdot C} nebo \bf{A=B/C} (například v=s/t) můžeme pomocí jednoduché pomůcky zjistit, jak vypadají vzorce pro \bf{B} a pro \bf{C}.
- Nakreslíme si trojúhelníkovou pyramidu (zatím prázdnou).
- Zakreslíme do ní pravou stranu rovnice (naše s/t), tak aby vypadala graficky stejně jako ve vzorci (dělení jako zlomek nad sebou, případně násobení vedle sebe v dolním patře).
- Na zbývající místo doplníme levou stranu vzorce.
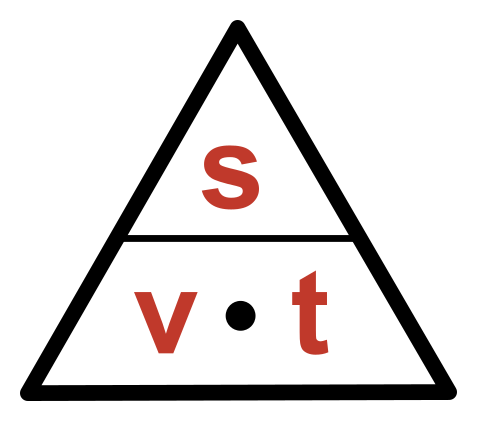
- Nyní stačí pro výpočet jakékoliv veličiny zakrýt tuto veličinu prstem a podívat se jak vypadají ostatní nezakryté.
Rychlost, dráha, čas: vzorce
Definice rychlosti v je dráha s za čas t. Matematicky zapsáno je to
v=\frac{s}{t}
Jde vlastně o rychlost průměrnou, ale v případě rovnoměrného pohybu i o okamžitou rychlost po celou dobu pohybu.
Příklad: Rychlost auta
- Auto ujelo 200 km za 4 h. Jakou udržovalo rychlost?
- Hledáme v a známe s a t. Použijeme tedy vzorec v=\frac{s}{t}
- Dosadíme do něj za s a t.
- v=\frac{200}{4}\,\mathrm {km/h}=50\,\mathrm {km/h}
- Auto udržovalo rychlost 50 km/h.
Můžeme počítat i s a t (vždy když známe zbývající dvě veličiny). Matematickou úpravou, resp. použitím vztahového trojúhelníku jsme odvodili vztahy pro dráhu
s=v\cdot t
Příklad: Dráha Tarzana
- Tarzan na liáně letí rychlostí 12 m/s po dobu 5 s než se rozplácne o strom. Jakou dráhu uletěl?
- Hledáme s a známe v a t. Použijeme tedy vzorec s=v\cdot t.
- Dosadíme za v a t.
- s=12 \cdot 5\,\mathrm m=60\,\mathrm m
- Tarzan se rozplácl po 60 m.
a pro čas
t=\frac{s}{v}.
Příklad: Letové hodiny stíhačky
- Stíhačka přeletěla 800 km rychlostí 1600 km/h. Jak dlouho letěla?
- Hledáme t a známe s a v. Použijeme tedy vzorec t=\frac{s}{v}
- Dosadíme do něj za s a v.
- t=\frac{800}{1600}\,\mathrm h=0{,}5\,\mathrm h
- Stíhačka letěla půl hodiny.
Rychlost, dráha, čas: pohyb tělesa
Ne vždy můžeme ihned dosadit do vzorců jako s=v\cdot t. Musíme totiž nejprve vyřešit drobné komplikace:
- Jednotky nesedí. Musíme převést na stejné jednotky, nebo alespoň tak abychom nekombinovali různé časové škály (např km/h se sekundami)
Autobus
- Autobus jel 15 minut rychlostí 40 km/h. Kolik toho ujel?
- V jednotce rychlosti jsou hodiny zatímco čas je v minutách. Musíme tedy převádět.
- Mohli bychom převádět na m/s a sekundy, ale bylo by to pracné.
- Lepší je převést čas na hodiny (výsledek vyjde v km).
- 15 minut → 0,25 h
- Konečně můžeme dosadit do s=v\cdot t.
- s=40\cdot 0{,}25 \,\mathrm{km} = 10\,\mathrm{km}
- Dráhy/časy složené z více částí. Celková dráha pohybu s je prostě součtem drah všech úseků s=s_1+s_2+\cdots. Totéž platí pro čas t=t_1+t_2+\cdots.
Triatlon
- Triatlonista zvládl závod za 2h. Přitom ujel 40 km na kole, 10 km běžel a 1,5 km plaval. Jakou měl průměrnou rychlost během celého závodu?
- Použijeme vzorec v=\frac{s}{t}, ale přímo známe jen čas t. Potřebujeme s.
- Celková dráha s je podle s=s_1+s_2+s_3
- Číselně s=40+10+1{,}5\,\mathrm {km}= 51{,}5\,\mathrm {km}.
- Už můžeme dosazovat v=\frac{51{,}5}{2}\,\mathrm {km/h}=25{,}75\,\mathrm {km/h}
Pro rychlost to ale neplatí! Průměrná rychlost více úseků dohromady se musí počítat jako v=\frac{s_1+s_2+\cdots}{t_1+t_2+\cdots}.
- Místo dráhy/času známe jen hodnoty na začátku a na konci. Neznáme dráhu přímo, ale známe polohy na trati na začátku a na konci pohybu. Podobně může být potřeba určit dobu pohybu t jako rozdíl časů (na hodinách) v okamžiku startu a cíle.
Sjezdy na dálnici
- Na dálnici jsme najeli nájezdem na 20. km a opustili ji sjezdem na 200. km. Jak dlouho jsme na ní strávili s rychlostí 90 km/h?
- Hledáme t. Přímo známe ale jen v.
- Dráhu s musíme určit jako rozdíl poloh na začátku a na konci.
- s=200-20\,\mathrm{km}=180\,\mathrm{km}
- Teprve nyní můžeme dosadit do t=\frac{s}{v}.
- t=\frac{180}{90}\,\mathrm{h}=2\,\mathrm{h}
Rychlost, dráha, čas: vzájemný pohyb těles
Pokud se pohybuje více těles, můžeme zkoumat jejich vzájemný pohyb.
Vzájemná rychlost dvou těles (těleso 1 a těleso 2) je rozdílem jejich rychlostí. Pokud budeme jednotlivé rychlosti značit indexy, můžeme pro vzájemnou rychlost použít v.
v=v_1-v_2
(pokud je důležitý směr a pokud rozlišujeme, zda jde o rychlost 1. tělesa vůči 2. nebo naopak, používá se také v_{12} resp v_{21})
Pokud se k sobě tělesa přibližují, určuje vzorec t=\frac{s}{v} čas setkání – dosazujeme do něj právě vzájemnou rychlost a počáteční vzdálenost těles (i pro tu používáme přímo písmeno s protože pro dráhy jednotlivých těles pravděpodobně použijeme s_1 a s_2).
Dráhy jednotlivých těles a místo setkání je možné poté dopočítat, když dosadíme do vzorce pohybu jednotlivých těles vypočtený čas setkání t (např. s_1=v_1\cdot t, nebo s_2=v_2\cdot t).
Nahoru
