Výpis souhrnů
Keplerovy zákony
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Keplerovy zákony
Tři Keplerovy zákony formuloval Johanes Kepler na základě pozorování pohybu planet kolem Slunce.
- 1. Keplerův zákon (zákon trajektorií) popisuje tvary oběžných drah planet ve Sluneční soustavě.
- 2. Keplerův zákon (zákon ploch) vysvětluje změny rychlosti planety během oběhu.
- 3. Keplerův zákon (zákon period oběhu) popisuje vztah mezi velikostí oběžné dráhy a dobou oběhu.
Druhý a třetí zákon platí obecně i pro jiná tělesa (např. komety) a pro obíhání kolem jiných gravitačních center (např. družice kolem Země).
Zajímavosti
Keplerovy zákony jsou vlastně zákony kinematiky (nepopisují mechanismus sil, které obíhání způsobují). To popsal až Isaac Newton, bylo to ale právě na základě Keplerových prací.
1. Keplerův zákon
První Keplerův zákon se nazývá také zákon trajektorií.
Planety se kolem Slunce pohybují po málo výstředných elipsách (tj. skoro kružnicích). Slunce se přitom nachází v jednom z ohnisek takové elipsy.
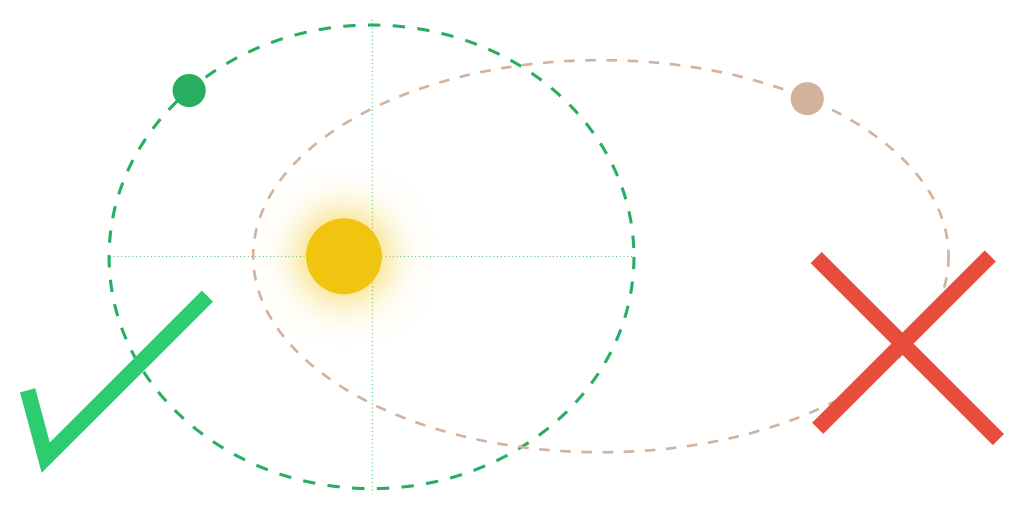
Vztahuje se jen na planety, neplatí např. pro komety.
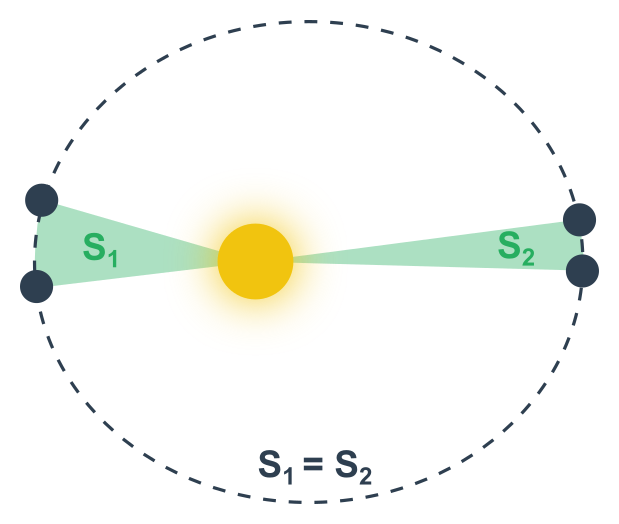
Nahoru2. Keplerův zákon
Druhý Keplerův zákon, neboli zákon ploch říká, že plocha opsaná průvodičem planety za jednotku času je stále stejná.
Kvantifikuje tak skutečnost, že se těleso blíže ke Slunci pohybuje rychleji. Konstantou totiž není rychlost, ani vzdálenost, ale právě plocha trojúhelníka o stranách „rychlost“ a „spojnice-se-sluncem“.
Matematicky zapsáno S=v\cdot r\cdot \sin \alpha = \mathrm{konst.} (kde \alpha je úhel mezi směrem rychlosti a spojnicí se Sluncem)
Příklad: Bývalá planeta Pluto v perihéliu a aféliu
V perihéliu je bývalá planeta Pluto vzdálena od Slunce 30 AU (astronomická jednotka) a v aféliu 49 AU. Kolikrát rychlejší je Pluto v periheliu než v aféliu?
- Poměr obou vzdáleností je \frac{r_\mathrm p}{r_\mathrm a}=\frac{30}{49}, tedy zhruba \frac{3}{5}.
- Poměr rychlostí je podle Keplerova zákona opačný. Tedy \frac{v_\mathrm p}{v_\mathrm a}\approx\frac{5}{3}.
- Rychlost v periheliu je tedy asi 1,67krát větší.
Pozn.: Konstantní je i plocha opsaná za jiný časový interval než klasická jednotka času. Například plocha opsaná průvodičem za 6 sekund bude taky neměnná (a bude 6krát větší než ta za jednu sekundu).
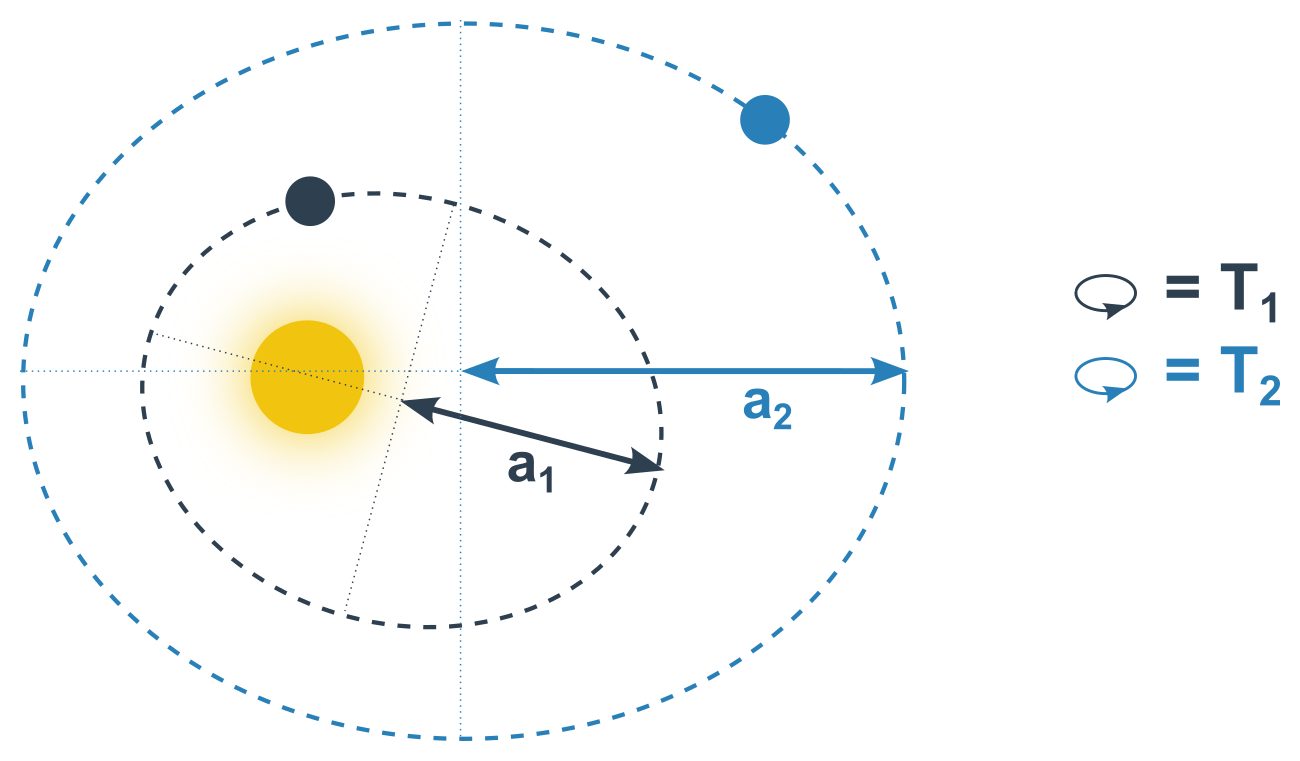
Nahoru3. Keplerův zákon
Třetím Keplerovým zákonem je zákon period oběhu:
Pro dvě planety obíhající kolem Slunce platí že, poměr druhých mocnin period oběhu je roven poměru třetích mocnin hlavních poloos oběžných drah. Matematicky zapsáno
\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}