Výpis souhrnů

Jednotky a veličiny

Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.

« Zpět na procvičování

Podtémata

Zápis čísel a jednotek
Převody jednotek
Vyjadřování veličin
Řecká abeceda

Zápis čísel a jednotek

Přejít ke cvičením na toto téma »

Fyzikální veličina je zapsána svojí hodnotou a jednotkou. Jednotka slouží k nastavení poměřování velikostí různých hodnot tak, že odpovídá hodnotě 1.

Příklad

Délka d je 15 cm

hodnota je 15
jednotka je centimetr (cm)
centimetr je určitá velikost v reálném světě, proti které je délka d 15násobná

Zápis jednotky

Jednotku zapisujeme buď jejím názvem (metr, gram, newton, hertz, …), nebo (zejména ve výpočtech) příslušnou zkratkou (m, g, N, Hz, …).

Pokud má základní jednotka velikost hodně mimo to, co měříme (např. jednotka je metr a chceme měřit tloušťku vlasu), používáme násobky jednotek:

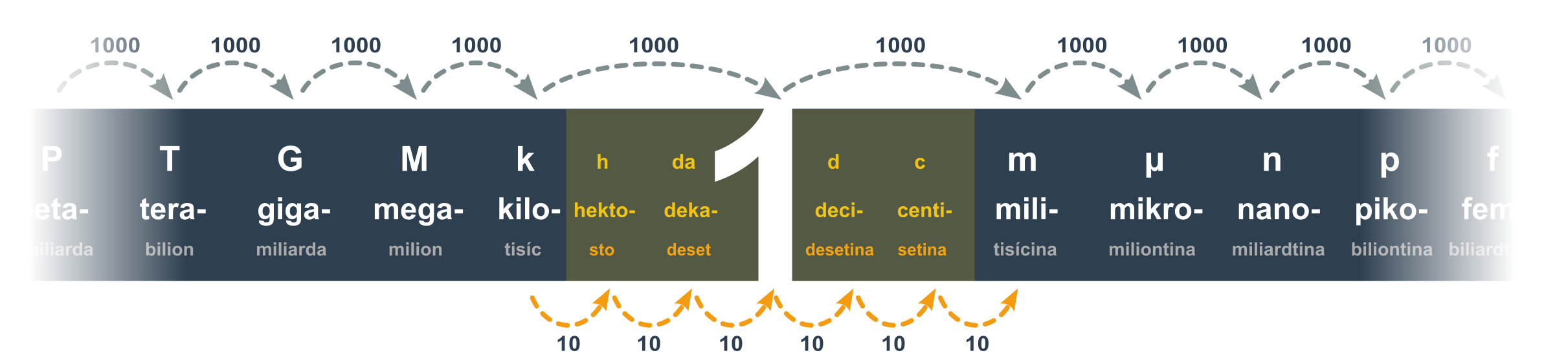
Celou jednotku pak tvoří předpona spojená s názvem jednotky (milimetr, kilogram, megahertz, …), v případě zkratky písmeno předpony spojené se zkratkou jednotky (mm, kg, MHz, …).

Zápis hodnoty

Hodnotu veličiny zapisujeme tak, jako čísla v matematice:

desetinné číslo (nejběžnější)
zlomek (může se hodit, ale ve fyzice spíš nepoužíváme)
složené číslo (ve fyzice téměř nikdy)
exponenciální tvar (výhodný u velkých/malých čísel a větších výpočtů)

Exponenciální (mocninný) tvar se tvoří rozdělením čísla na součin čísla mezi 1 a 10 a odpovídající mocniny deseti. Např.: 0,02 je 2 ⋅ 10⁻².

Příklady

1,25 (desetinný) = 5/4 (zlomek) = 1 a 1/4 (složené) = 1,25 ⋅ 10⁰ (exp)
64 000 (desetinný) = 6,4 ⋅ 10⁴ (exp)
0,000 000 89 (desetinný) = 8,9 ⋅ 10⁻⁷ (exp)

Převody jednotek

Přejít ke cvičením na toto téma »

Pokud chceme veličinu převést na jinou jednotku (jiný násobek), mění se i číselná hodnota veličiny (protože vyjadřuje kolikrát je tato veličina větší než jedna jednotka).

Pokud přecházíme na vyjádření v menší jednotce (např. z metrů na milimetry), musí se hodnota zvětšit. Tolikrát, kolikrát je nová jednotka menší. A naopak.

Přehled poměrů mezi jednotlivými násobky základních jednotek:

Příklad převodu hmotnosti

Hmotnost m je 1500 g. Převádíme na kg.

kg je 1000krát větší jednotka než mg
hodnota se proto 1000krát zmenší
po převedení máme 1,5 kg

Jednotky s mocninami

Pro převody jednotek s mocninami platí, že poměr v tabulce výše se násobí tolikrát, kolikátou mocninu jednotky máme.

Příklad s plošnými jednotkami

Plocha S je 3 m². Převádíme na cm².

cm je 100krát menší jednotka než m
jednotky jsou ve druhé mocnině (m²)
cm² je tedy (100⋅100)krát menší jednotka než m²
hodnota se proto 10 000krát zvětší
po převedení máme 30 000 cm²

Příklad s objemovými jednotkami

Objem V je 150 000 mm³. Převádíme na dm³.

dm je 100krát větší jednotka než mm
jednotky jsou ve třetí mocnině (dm³)
dm³ je tedy (100⋅100⋅100)krát větší jednotka než mm³
hodnota se proto 1 000 000krát zmenší
po převedení máme 0,15 dm³

Vyjadřování veličin

Přejít ke cvičením na toto téma »

Návod na úpravy rovnic za účelem vyjádření veličin:

Řecká abeceda

Přejít ke cvičením na toto téma »

Řecká písmena se ve fyzice používají jako doplnění klasické latinky pro označení řady různých veličin. Některá písmena (například \varphi) se používají často a dokonce i pro více veličin, jiná (jako \zeta) bychom obtížně hledali i ve vysokoškolských učebnicích.

\alpha	\Alpha	alfa	\iota	\Iota	ióta	\rho	\Rho	ró
\beta	\Beta	beta	\kappa	\Kappa	kappa	\sigma	\Sigma	sigma
\gamma	\Gamma	gama	\lambda	\Lambda	lambda	\tau	\Tau	tau
\delta	\Delta	delta	\mu	\Mu	mí	\upsilon	\Upsilon	ypsilon
\varepsilon	\Epsilon	epsilon	\nu	\Nu	ný	\varphi	\Phi	fí
\zeta	\Zeta	zéta	\xi	\Xi	ksí	\chi	\Chi	chí
\eta	\Eta	éta	\omicron	\Omicron	omikron	\psi	\Psi	psí
\theta	\Theta	théta	\pi	\Pi	pí	\omega	\Omega	omega

Některé znaky mohou mít více uznávaných (a poměrně odlišných) podob. Setkáme se zejména s těmito:

malé fí – \phi i \varphi
malé epsilon – \epsilon i \varepsilon
malé ró – \rho \varrho
malé kappa – \kappa i \varkappa

Výpis souhrnů

Jednotky a veličiny

Podtémata

Zápis čísel a jednotek

Zápis jednotky

Zápis hodnoty

Převody jednotek

Jednotky s mocninami

Vyjadřování veličin

Řecká abeceda

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?