Čeština
Matematika
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Biologie
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Rozhodovačka
Otázky
Slepé mapy
Pexeso
Přesouvání
Rozřazovačka
Řazení
Poznávačka
Krok po kroku
Vpisování
Porozumění
Doplňování textu
Pojmy ve větách
Označování
Situace
Poznávání zvuků
Křížovky
Roboti
Tetris
Tipovačka
Týmovka
Závody
Odkrývačka
Můj účet
Odhlásit seVýpis souhrnů
Proudění kapalin a plynů
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Rovnice kontinuity
U proudění tekutin definujeme tzv. objemový průtok Q_V. Je to objem tekutiny, který proteče trubkou za jednotku času. Jednotkou je tedy m³/s a platí:
Q_V=\frac{V}{t}
Příklad: ropovod
Jaký byl průtok ropovodem, pokud za 1 minutu proteklo 30 m³ ropy?
- Známe V i t.
- Čas t není v základních jednotkách, musíme jej tedy převést na sekundy t= 60\,\mathrm s
- Dosadíme do Q_V=V/t
- Q_V=30/ 60 \,\mathrm {m^3/s}=0{,}5 \,\mathrm {m^3/s}.
- Průtok je 0{,}5 \,\mathrm {m^3/s} ropy.
Objem V je ale roven součinu průřezu trubice S a posunu kapaliny o dráhu s. Po dosazení máme Q_V=\frac{S\cdot s}{t}.
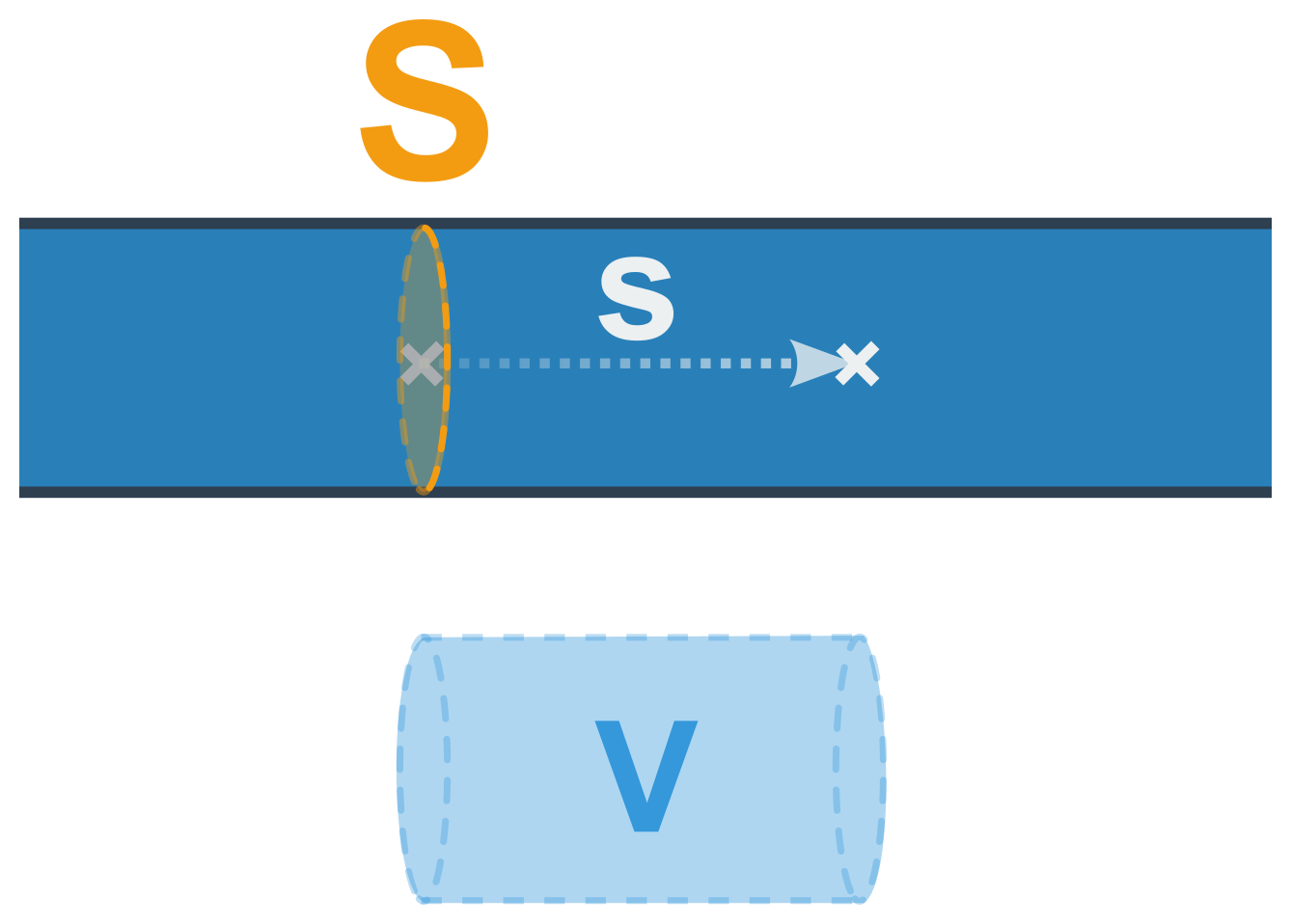
Víme přitom, že \frac{s}{t} je klasická definice rychlosti, tedy i rychlosti proudění v. Pak můžeme průtok zapsat ekvivalentní rovnicí:
Q_V=S\cdot v
Příklad: Lipno
Jaký průtok vody míří na turbínu vodní elektrárny Lipno I, pokud v její 15 m² přívodní šachtě proudí voda rychlostí 2 m/s?
- Známe S i v a to v základních jednotkách.
- Stačí tedy dosadit dosadit do Q_V=S\cdot v
- Q_V=15\cdot 2 \,\mathrm {m^3/s}=30 \,\mathrm {m^3/s}
- Průtok je 30 \,\mathrm {m^3/s}.
Protože jsou kapaliny nestlačitelné, musí být průtok Q_V v uzavřeném plném potrubí všude stejný (jinak by se někde musela hromadit).
Pokud tedy porovnáme dvě místa (Q_{V{,}1}=Q_{V{,}2}) a dosadíme za jednotlivé průtoky, vznikne známý vzorec rovnice kontinuity:
S_1\cdot v_1=S_2\cdot v_2
Příklad: stále stejně tlusté potrubí
Jak se mění rychlost ideální kapaliny při průchodu stále stejně tlustým potrubím?
- Nabízí se odpověď „všude stejná“. Ověříme to.
- Pro dvě místa v trubici platí S_1\cdot v_1=S_2\cdot v_2.
- Oba průřezy S_1 i S_2 jsou stejné, označme je tedy jednotně jako S.
- Máme S\cdot v_1=S\cdot v_2. V této rovnici můžeme krátit S.
- Dostaneme v_1=v_2. Tedy i rychlosti musí být stejné.
Příklad: přechod potrubí na třikrát větší průřez
Jak se změní rychlost ideální kapaliny při rozšíření potrubí na trojnásobný průřez?
- Nejprve přiřadíme jednotlivým místům v potrubí označení: užší část bude (1) a širší (2).
- Platí S_1\cdot v_1=S_2\cdot v_2.
- Víme že S_2=3\cdot S_1. Dosadíme to do rovnice.
- S_1\cdot v_1=3\cdot S_1\cdot v_2. Můžeme krátit S_1.
- Dostaneme v_1=3\cdot v_2. Hledáme ale rychlost v_2.
- Dělíme tedy 3 a dostaneme v_2=\frac{1}{3} v_1.
- Rychlost tedy bude třetinová.
Zajímavosti
- Přibližně platí i pro volně proudící kapalinu (řeka a její koryto).
- Někdy přibližně platí pro plyny (jsou stlačitelné).
- Obdobné rovnice kontinuity platí například i v elektřině (1. Kirchhoffův zákon).
- Rovnice V=S\cdot s je spolehlivá jen pro malé s (mohl by se změnit průměr trubice). Naštěstí rovnice Q_V=S\cdot v je už platná obecně.
Bernoulliho rovnice
Bernoulliho rovnice popisuje souvislost mezi tlakem p v kapalině (o hustotě \rho) a rychlostí jejího proudění v. Podél jedné proudnice platí:
\frac{1}{2}\rho v^2+p = \mathrm{konst.}
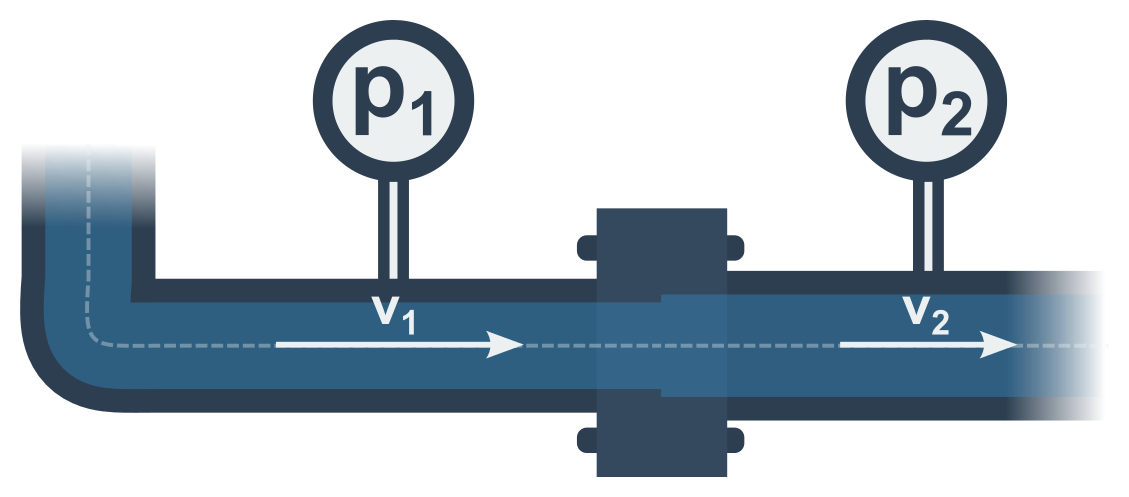
Pro dvě místa na téže proudnici tedy platí (pro konstantní hustotu):
\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2
Pro jednoduchost obvykle definujeme Bernoulliho rovnici pro vodorovnou uzavřenou trubku.
Jak by to bylo pro nevodorovnou trubku?
Pro nevodorovnou trubku bychom museli do celkového tlaku započítávat i hydrostatický tlak p_h.
Bernoulliho rovnice vlastně říká, že zvýšením rychlosti proudění poklesne tlak. Tento princip platí i pro libovolné neturbulentní proudění kapaliny nebo plynu. Matematický vzorec sice v takovém případě neplatí přesně, ale jako odhad se hodí.
Tohoto principu se využívá v řadě případů, kde chceme vůči okolnímu prostředí vytvořit podtlak (fixírka, některé typy vývěv, profil křídla letadel).
Zajímavosti
Bernoulliho rovnice je vlastně rovnice zachování energie na jednotku objemu. Po vynásobení objemem je to ještě patrnější – získáte \frac{1}{2}m v^2 (kinetická energie) a p\cdot V=p\cdot S\cdot s=F\cdot s (práce/potenciální energie).
Vytékání kapaliny malým otvorem
Pomocí Bernoulliho rovnice (\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2) můžeme odvodit rychlost tryskání vody z (malého) otvoru v nějaké nádobě.
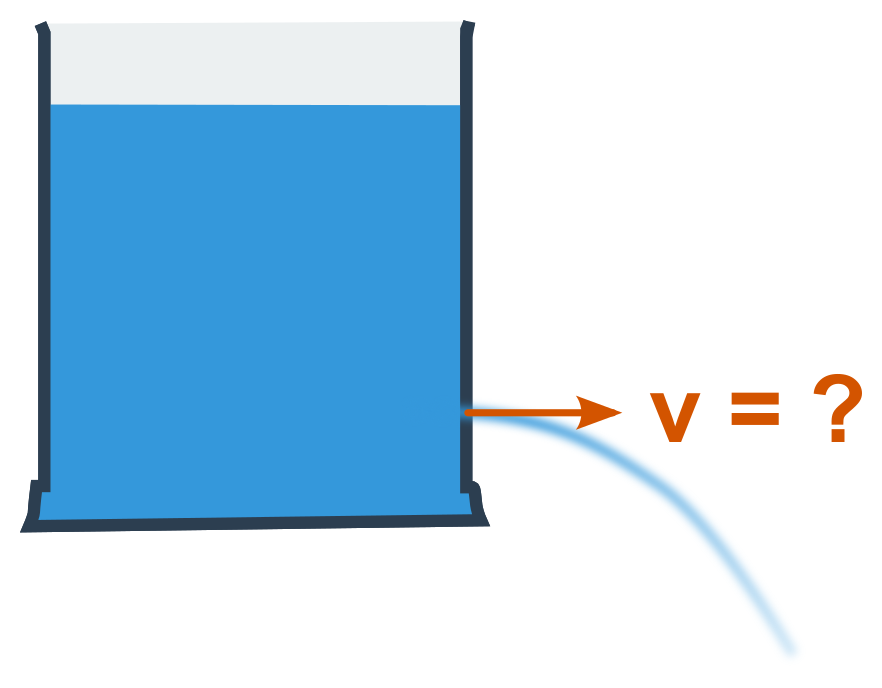
Zevnitř (index 1) je rychlost prakticky nulová a vně (index 2) je zase nulový tlak (pokud od obou stran odečteme atmosférický tlak). Po dosazení těchto nul do rovnice výše dostaneme p_1 = \frac{1}{2}\rho v_2^2.
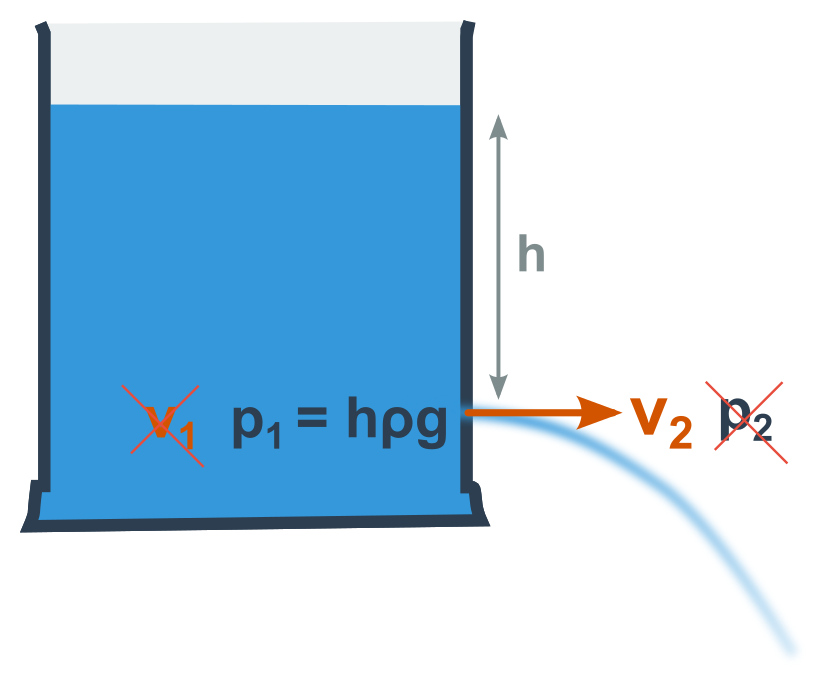
Tlak p_1 je vlastně hydrostatický tlak v nádobě (h\rho g) a rychlost zůstala jen jedna, nemusíme ji tedy indexovat. Máme h\rho g=\frac{1}{2}\rho v^2, z čehož vyjádříme rychlost:
v = \sqrt{2 h g}
Příklad: dvojnásobná hloubka
- Bude z otvoru v dvojnásobné hloubce nebude stříkat voda dvakrát rychleji?
- Podle vzorce v = \sqrt{2 h g} závisí rychlost na odmocnině z hloubky.
- Pokud tedy změníme h na 2h, dostaneme v = \sqrt{2\cdot 2 h g}= \sqrt{2}\cdot \sqrt{2 h g}.
- Rychlost tedy bude jen \sqrt 2-krát větší.
Příklad: stav beztíže
- Jaká bude rychlost stříkání vody z děravé lahve ve stavu beztíže?
- Ve stavu beztíže je g nulové.
- Do v = \sqrt{2 h g} tedy dosazujeme nulu. A součin s nulou je nulový celý.
- A odmocnina z nuly je nula. Rychlost tedy bude nulová – ve stavu beztíže voda samovolně nevytéká.
